

 Previous: 3.3 Monte-Carlo Method
Up: 3.3 Monte-Carlo Method
Next: 3.3.2 Nuclear Stopping Process
Previous: 3.3 Monte-Carlo Method
Up: 3.3 Monte-Carlo Method
Next: 3.3.2 Nuclear Stopping Process
3.3.1 Energy Loss Mechanisms
Entering the target an ion starts loosing energy by interacting with the nuclei
and the electrons of the target material. On entrance the kinetic ion energy is
in the keV range which results in a speed of some hundred m/s. The final
point of the ion trajectory is reached when the kinetic energy of the particle
reaches the thermal energy, which is of the order of 35 meV. Assuming a constant
slow down, the time an ion needs to come to rest (ballistic time) can be
estimated by
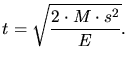 |
(3.50) |
It is of the order of 10 s if the ion trajectory length
s if the ion trajectory length 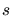 is about
1
is about
1 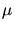 m and the implantation energy
m and the implantation energy 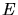 is in the hundred keV range.
is in the hundred keV range. 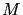 is the
ion mass. For several application the ballistic time will be even shorter.
is the
ion mass. For several application the ballistic time will be even shorter.
In the general case the energy loss would have to be calculated by solving the
Schrödinger equation with the Hamiltonian operator
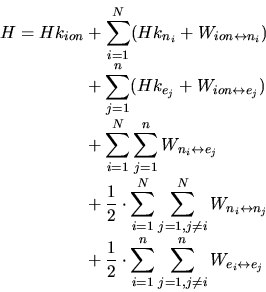 |
(3.51) |
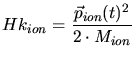 |
(3.52) |
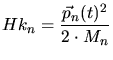 |
(3.53) |
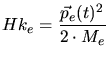 |
(3.54) |
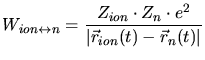 |
(3.55) |
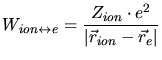 |
(3.56) |
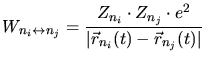 |
(3.57) |
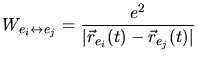 |
(3.58) |
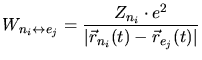 |
(3.59) |
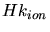 ,
, 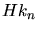 ,
, 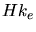 are the kinetic energies of the ion, the target
nuclei and the target electrons,
are the kinetic energies of the ion, the target
nuclei and the target electrons, 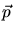 are their moments, and
are their moments, and 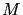 are their
masses. Beside the kinetic energies the interaction potentials
are their
masses. Beside the kinetic energies the interaction potentials 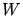 between the
ion and the target nuclei (
between the
ion and the target nuclei (
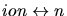 ) and electrons
(
) and electrons
(
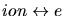 ) are considered. Finally the interactions of the target
nuclei and electrons among themselves (
) are considered. Finally the interactions of the target
nuclei and electrons among themselves (
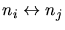 ,
,
 ,
,
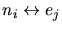 ) are taken into
account.
) are taken into
account.  ,
, 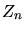 are the charges of the ion and of the nuclei, and
are the charges of the ion and of the nuclei, and
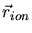 ,
, 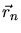 ,
, 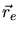 are the coordinates of the ion, the
nuclei and the electrons.
are the coordinates of the ion, the
nuclei and the electrons.
Since a rigorous treatment of this problem is not feasible several assumptions
have to be made to provide an appropriate theoretical background.
First of all is the old assumption made by Bohr [10] to separate
the interaction of the ion with the nuclei of the target from the interaction
with the electrons of the target. The interaction of the ion with the nuclei
(nuclear stopping process) can be treated as an elastic collision process,
while the interaction with the electrons can be treated as an inelastic process
without any scattering effects (electronic stopping process). The total
stopping process can be modeled as as sequence of alternating nuclear and
electronic stopping processes.


 Previous: 3.3 Monte-Carlo Method
Up: 3.3 Monte-Carlo Method
Next: 3.3.2 Nuclear Stopping Process
Previous: 3.3 Monte-Carlo Method
Up: 3.3 Monte-Carlo Method
Next: 3.3.2 Nuclear Stopping Process
A. Hoessiger: Simulation of Ion Implantation for ULSI Technology
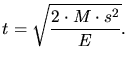
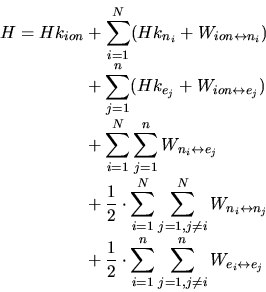
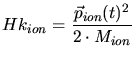
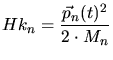
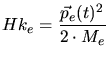
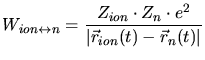
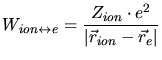
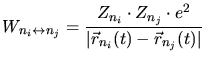
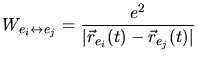
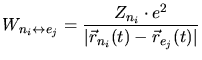
![]()
![]()
![]()
![]() Previous: 3.3 Monte-Carlo Method
Up: 3.3 Monte-Carlo Method
Next: 3.3.2 Nuclear Stopping Process
Previous: 3.3 Monte-Carlo Method
Up: 3.3 Monte-Carlo Method
Next: 3.3.2 Nuclear Stopping Process