

 Previous: 3.3.1 Energy Loss Mechanisms
Up: 3.3 Monte-Carlo Method
Next: 3.3.2.1 Interatomic Screening Potential
Previous: 3.3.1 Energy Loss Mechanisms
Up: 3.3 Monte-Carlo Method
Next: 3.3.2.1 Interatomic Screening Potential
The interaction of a moving charged particle with nuclei of a solid can be
described by a series of classical elastic scattering processes. It is assumed
by the Monte-Carlo method that only two particles (the ion and one target
nucleus) are considerably involved in one scattering processes. This is called
the binary collision approximation), which reduces the multi particle
problem to a classical elastic two particle problem which is characterized by
the conservation of energy (3.60) and momentum
(3.61) (3.62). The non-relativistic
conservation laws can be used because the particle velocities are of the order
of 0,1% of the speed of light for typical ion implantation applications.
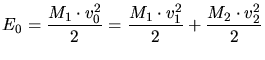 |
(3.60) |
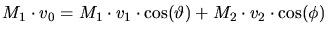 |
(3.61) |
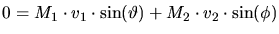 |
(3.62) |
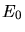 is the initial kinetic energy of the two particle system,
is the initial kinetic energy of the two particle system, 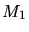 ,
, 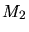 are
the masses of the particles.
are
the masses of the particles.
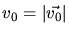 is the speed of the moving
particle before, while
is the speed of the moving
particle before, while
 is its velocity after the scattering
process.
is its velocity after the scattering
process.
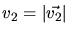 is the final speed of
the initially resting particle.
is the final speed of
the initially resting particle. 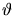 and
and 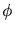 are the deflection
angles. Besides the initial energy and the initial momentum the scattering
process is characterized by the impact parameter
are the deflection
angles. Besides the initial energy and the initial momentum the scattering
process is characterized by the impact parameter 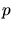 which is the minimum
distance of the two particles if they would pass without
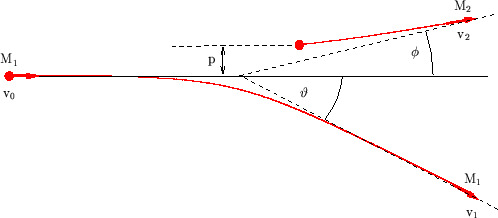
interaction. Fig. 3.2 schematically shows the behavior of an
elastic two particle scattering process.
which is the minimum
distance of the two particles if they would pass without
interaction. Fig. 3.2 schematically shows the behavior of an
elastic two particle scattering process.
Figure 3.2:
Two particle scattering process in the laboratory system.
 |
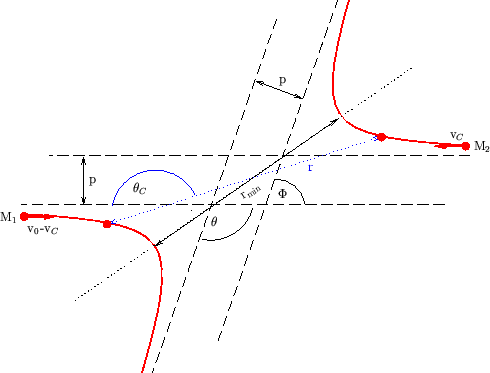
By transforming the equations to the center-of-mass coordinates the two particle
problem can be converted to that of a single particle moving in a central
potential (Fig. 3.3).
Figure 3.3:
Two particle scattering process in the center-of-mass coordinate system.
 |
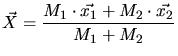 |
(3.63) |
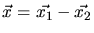 |
(3.64) |
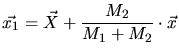 |
(3.65) |
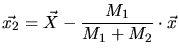 |
(3.66) |
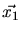 ,
, 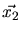 are the coordinates in the laboratory system while
are the coordinates in the laboratory system while
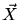 is the position of the center of mass and
is the position of the center of mass and 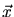 are the relative
coordinates of the particles. The velocity of the center-of-mass
are the relative
coordinates of the particles. The velocity of the center-of-mass 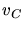 is
constant.
is
constant.
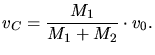 |
(3.67) |
Introducing a reduced mass 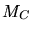 (3.67) can be reformulated to
(3.67) can be reformulated to
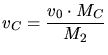 |
(3.68) |
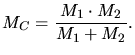 |
(3.69) |
The velocities of the particles in the center-of-mass system at the beginning of
the scattering event are 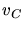 (particle 2) and
(particle 2) and
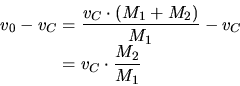 |
(3.70) |
(particle 1). The total momentum is
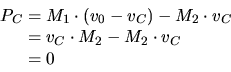 |
(3.71) |
and therefore the particle velocities remain unchanged after the collision. The
kinetic energy of the particles is
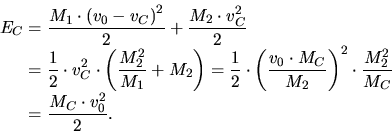 |
(3.72) |
Using these relations the kinetic energy transfer 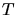 from the incident particle
to the target can be derived as a function of the scattering angle
from the incident particle
to the target can be derived as a function of the scattering angle 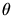 (Fig. 3.3) which is related to the angles
(Fig. 3.3) which is related to the angles 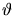 and
and 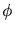 in the laboratory system (Fig. 3.2) by
in the laboratory system (Fig. 3.2) by
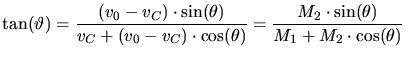 |
(3.73) |
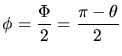 |
(3.74) |
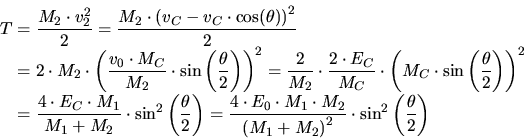 |
(3.75) |
In order to rigorously simulate the motion of a particle through mater not only the
transfered energy as a function of the scattering angle but also the scattering angle as
a function of the impact parameter has to be calculated, which requires a
rigorous solution of the equation of motion. A very convenient way is the
derivation by using Lagrangian mechanics. The Lagrange function in the
center-of-mass coordinates ((3.63) and (3.64)) is
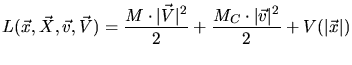 |
(3.76) |
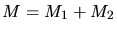 |
(3.77) |
Using the Lagrange equation (3.78) gives two independent equations of
motion, one for the center-of-mass (3.79) and one for a particle in
the central potential
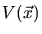 (3.80), which represents the
motion in the center-of-mass system.
(3.80), which represents the
motion in the center-of-mass system.
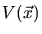 is equivalent to the
interaction potential of the particles.
is equivalent to the
interaction potential of the particles.
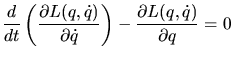 |
(3.78) |
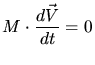 |
(3.79) |
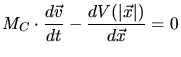 |
(3.80) |
For a particle moving in a central potential the energy 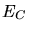 and the angular
momentum
and the angular
momentum 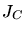 is constant. Using these conservation law the equation of motion
can easily be solved in polar coordinates. The initial energy and the initial
angular momentum are
is constant. Using these conservation law the equation of motion
can easily be solved in polar coordinates. The initial energy and the initial
angular momentum are
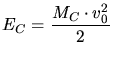 |
(3.81) |
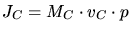 |
(3.82) |
while they can be described during the motion by
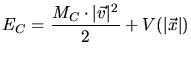 |
(3.83) |
 |
(3.84) |
(3.83) and (3.84) can be expressed in polar
coordinates by
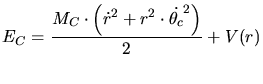 |
(3.85) |
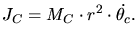 |
(3.86) |
Combining (3.83) and (3.84) with
(3.81) and (3.82) gives the equation of motion in
polar coordinates.
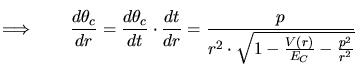 |
(3.87) |
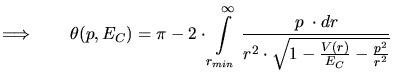 |
(3.88) |
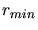 is the distance of minimum approach between the particles and it is
determined by the real root of the denominator of (3.87). An
interpretation of the coordinates of the central potential scattering problem is
denoted by the dotted arrow in Fig. 3.3.
is the distance of minimum approach between the particles and it is
determined by the real root of the denominator of (3.87). An
interpretation of the coordinates of the central potential scattering problem is
denoted by the dotted arrow in Fig. 3.3.
The major problem that arises when modeling this scattering process is to
determine the interaction potential 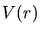 between the ion and the target. In
principle it is a repulsive Coulomb potential due to the positive charges of the
cores. This Coulomb potential is screened by the surrounding electrons. The
effect of the electrons can be described by adding a dimensionless screening function
between the ion and the target. In
principle it is a repulsive Coulomb potential due to the positive charges of the
cores. This Coulomb potential is screened by the surrounding electrons. The
effect of the electrons can be described by adding a dimensionless screening function
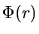 to the Coulomb potential.
to the Coulomb potential.
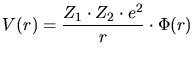 |
(3.89) |
Subsections


 Previous: 3.3.1 Energy Loss Mechanisms
Up: 3.3 Monte-Carlo Method
Next: 3.3.2.1 Interatomic Screening Potential
Previous: 3.3.1 Energy Loss Mechanisms
Up: 3.3 Monte-Carlo Method
Next: 3.3.2.1 Interatomic Screening Potential
A. Hoessiger: Simulation of Ion Implantation for ULSI Technology
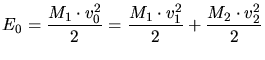
![]() (particle 2) and
(particle 2) and
![]() and the angular
momentum
and the angular
momentum ![]() is constant. Using these conservation law the equation of motion
can easily be solved in polar coordinates. The initial energy and the initial
angular momentum are
is constant. Using these conservation law the equation of motion
can easily be solved in polar coordinates. The initial energy and the initial
angular momentum are
![]() between the ion and the target. In
principle it is a repulsive Coulomb potential due to the positive charges of the
cores. This Coulomb potential is screened by the surrounding electrons. The
effect of the electrons can be described by adding a dimensionless screening function
between the ion and the target. In
principle it is a repulsive Coulomb potential due to the positive charges of the
cores. This Coulomb potential is screened by the surrounding electrons. The
effect of the electrons can be described by adding a dimensionless screening function
![]() to the Coulomb potential.
to the Coulomb potential.