3.3.2.1 Interatomic Screening Potential

It is possible to extract the interatomic screening potential from experimental data [43], but this technique can just be applied to a limited number of atom types. More successfully is to perform a simplified quantum-mechanical calculation of the penetration of two atoms as suggested by Gombas [28]. Based on this method various interatomic potential have been calculated [88], [92] which mainly differ by the the atom models and the corresponding electron charge distributions of the atoms. Classical charge distributions such as those of Bohr [11], Thomas-Fermi [77], Lenz-Jensen [42], [49] and Moliére [58] have been used for the calculations as well as quantum-mechanical charge distributions derived by the Hartree-Fock approximation [23] for isolated atoms or by solid-state atomic models [47].

The interaction potential is calculated by assuming that the charge distributions of the atoms remain unchanged during the penetration of the electron spheres and that the charge distributions are spherically symmetric. The following contributions to the potential energy are considered.

• The classical terms of Coulomb interaction between
  • the nuclei of the particles
  • the electrons of the particles
  • the nuclei and the electrons of the other particle
• The increase of the kinetic electron energy due to the Pauli exclusion principle and an increase of the exchange energy in the areas where the electron spheres overlap. The higher electron concentrations in these regions require a higher electronic kinetic energy which is approximated by the kinetic energy of a degenerated free electron gas.

Ziegler, Biersack and Littmark have performed potential calculations for a wide range of particle pairs (522 atoms pairs). They assumed solid state charge distributions for both particles, which were constructed by using a Hartree-Fock-Slater [23] method or in some cases by local density approximations for exchange and correlation effects as proposed in [59].

To be able to apply the solid state charge distribution to the semi quantum-mechanical model the real, anisotropic solid state charge distribution was transformed to a spherical symmetric distribution by averaging over all spatial directions.

Figure 3.4: Universal screening potential as a function of the reduced radius $x = \frac {r}{a_U}$.

Figure 3.5: Reduced radius as function of the real radius.

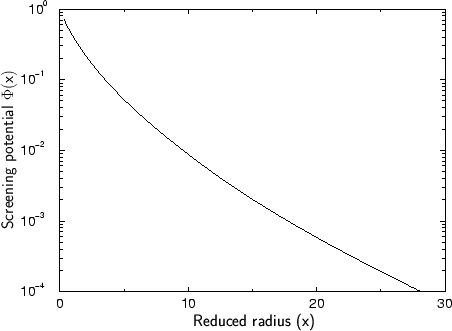
On the basis of their calculations they could extract an approximate analytical expression for the dimensionless screening potential, the universal screening potential (USP) $\Phi(x)$ plotted in Fig. 3.4 [92]. This potential should be suitable for arbitrary atom pairs.

$$\begin{split}\Phi(x) &= 0,1818\cdot e^{-3,2\cdot x} + 0,5099\... ...e^{-0,4028\cdot x} + 0,02817\cdot e^{-0,2016\cdot x}\end{split}$$ (3.90)

The universal screening potential is a functions of the dimensionless reduced radius $x$ which is related to the real radius by the scaling length $a_U$ suggested by Ziegler, Biersack and Littmark, depending on the charges of the involved atoms. The unit of the scaling length in (3.92) is Å.

$$x = \frac{r}{a_U}$$ (3.91)

$$a_U = 0,8854\cdot \frac{a_0}{Z_1^{0,23} + Z_2^{0,23}}$$ (3.92)

$a_0 = 0,529$ Å is the Bohr radius. A graphical illustration of the relation between the reduced radius and the real radius is given in Fig. 3.5 for a variety of atom pairs relevant for ion implantation simulation.

Comparing the universal screening to the simulation results which were the base for the extraction of this analytical approximation function it can be said that the potential is approximately valid for almost all atom pairs. The deviation between the 522 calculated potentials and the fitted universal screening potential is approximately 18 % as long as the potential energy is above 2 eV. For lower potential energies the deviation is significantly larger which probably limits the use of the universal screening potential.