3.3.3 Electronic Stopping Process

Modeling the electronic stopping process is very complicated, because several physical effects contribute to the inelastic energy loss.

• Excitation of conduction and band electrons (non-localized weakly bound electrons).
• Excitation or ionization of target atoms (promotion of localized electrons).
• Ionization or electron capture of the projectile.

All these effects occur due to core-electron and electron-electron interaction.

The most widely used technique for modeling the electronic stopping process is based on the local density approximation. It assumes that in each (infinitesimal) volume element of the target the interaction between the projectile and the target electrons depends only on one property of the target, namely the local electron density within this volume element. The local electron density 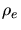$\rho_e$ at a position 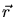$\vec{r}$ is

$$\rho_e = \sum\limits_i^{electrons} \vert\phi_i(\vec{r})\vert^2.$$ (3.99)

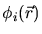$\phi_i(\vec{r})$ are the single electron wave-functions of all electrons in the target. Furthermore the local density approximation assumes that the interaction of the moving ion with the electrons in a certain volume element equals the interaction of the moving point charge with electrons in an infinite free electron gas with the same homogeneous electron density. An infinite free electron gas is a theoretical model which assumes that electrons with a definite electron density are homogeneously distributed in the whole space and that no forces act on the electrons.

The local density approximation neglects:

• Effects arising from a gradient in the target electron density in the sphere of influence of the projectile
• The influence of the solid state energy spectrum of the target electrons, because free electrons are characterized by a continuous energy spectrum, because no force act on the electrons.

Applying this approximation the remaining problems are to derive the energy loss of a point charge in a free electron gas and to determine an effective charge of the point charge in a free electron gas which optimally represents the behavior of the projectile in the solid.