

 Previous: 3.3.3.2 Effective Charge of
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.4 Thermal Lattice Vibration
Previous: 3.3.3.2 Effective Charge of
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.4 Thermal Lattice Vibration
3.3.3.3 Empirical Electronic Stopping Model
On the basis of the Lindhard electronic stopping model Hobler et al. proposed an
empirical stopping model [36] for the implantation into crystalline
silicon where the local electron densities in the target are not explicitly
considered for the calculation of the stopping power. Instead an impact parameter
of the ion is defined.
The model is composed of a non-local part which dominates in case of
large impact parameters (channeling ions), and a local part which describes
the close collisions.
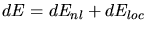 |
(3.126) |
The non-local part 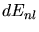 is derived from the simplified velocity proportional
stopping power calculated by Lindhard (3.119).
is derived from the simplified velocity proportional
stopping power calculated by Lindhard (3.119).
![\begin{displaymath}\begin{split}dE_{nl} &= N\cdot k_{corr}\cdot k\cdot \sqrt{E}\...
...ht)\cdot \exp\left(-\frac{p_{max}}{a}\right)\right] \end{split}\end{displaymath}](img363.gif) |
(3.127) |
The coefficient 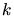 considers as well the properties of the ion
species as of the target material. A value proposed for
considers as well the properties of the ion
species as of the target material. A value proposed for 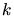 in [51] is
in [51] is
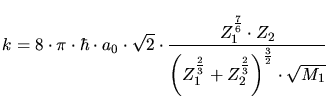 |
(3.128) |
The local part  is exponentially proportional to the impact
parameter as proposed by Oen and Robinson [61]. It is related to a
single collision event and therefore a discontinuous contribution to the total
energy loss.
is exponentially proportional to the impact
parameter as proposed by Oen and Robinson [61]. It is related to a
single collision event and therefore a discontinuous contribution to the total
energy loss.
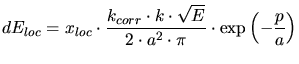 |
(3.129) |
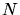 is the target atom density,
is the target atom density, 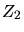 is the charge of the target atoms,
is the charge of the target atoms, 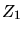 and
and 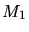 are the charge and the mass of the implanted particle,
are the charge and the mass of the implanted particle, 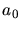 is the Bohr
radius, and
is the Bohr
radius, and 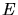 the energy of the particle.
the energy of the particle. 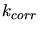 ,
, 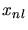 ,
,  ,
,
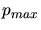 and
and 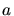 are empirical parameters.
are empirical parameters.
As indicated by Lindhard the electronic stopping power is
only proportional to the ion velocity 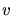 for low ion velocities. A velocity of
for low ion velocities. A velocity of
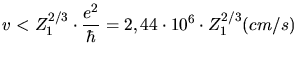 |
(3.133) |
can be considered as a limit. For higher energies the stopping power reaches a
maximum before it decreases again. Worth mentioning is that experimentally
determined stopping power functions do not yield a stopping power which is
proportional to the ion velocity for very low ion energies 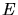 . Instead an
electronic stopping power being proportional to
. Instead an
electronic stopping power being proportional to 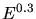 up to
up to 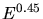 [2], [18] is reported. This fact has to be considered as a
source for small errors when applying the electronic stopping power law derived
by Lindhard. Fig. 3.8 schematically shows the functional
behavior of the electronic stopping power over the whole energy range.
[2], [18] is reported. This fact has to be considered as a
source for small errors when applying the electronic stopping power law derived
by Lindhard. Fig. 3.8 schematically shows the functional
behavior of the electronic stopping power over the whole energy range.
Figure 3.8:
Functional behavior of the electronic stopping power as a function of
the ion velocity.
![\begin{figure}\begin{center}
\psfrag{Electronic stopping power}[c][c]{\LARGE\sf ...
...}{\includegraphics{fig/physics/ElectronicStopping.eps}}}\end{center}\end{figure}](img381.gif) |
Table 3.3:
The electronic stopping power is only proportional to the velocity up
to a maximal energy. These maximal energies are summarized for several ion species.
| Ion species |
Energy limit (MeV) |
| Boron |
2.2 |
| Nitrogen |
4.6 |
| Fluorine |
8.7 |
| Phosphorus |
28.0 |
| Arsenic |
194.1 |
| Indium |
495.5 |
|
As a model for energies around the maximum of the stopping power an interpolation
between the velocity proportional stopping power  and a stopping formula
derived by Bethe and Bloch
and a stopping formula
derived by Bethe and Bloch 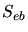 [1], [4],
[6], [39], which is valid for high ion energies, is
suggested in [75].
[1], [4],
[6], [39], which is valid for high ion energies, is
suggested in [75].
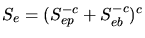 |
(3.134) |
According to the Bethe-Bloch theory the electronic stopping power for high ion
velocities is determined by ([73])
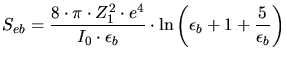 |
(3.135) |
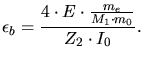 |
(3.136) |
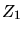 and
and 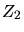 are the core charges of the ion and of the target,
are the core charges of the ion and of the target, 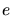 is the
elementary charge,
is the
elementary charge, 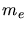 is the electron mass,
is the electron mass, 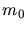 the atomic mass unit,
the atomic mass unit, 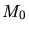 the relative atom mass of the ion, and
the relative atom mass of the ion, and 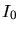 the so called Bloch constant
determined by (3.137) in units of eV.
the so called Bloch constant
determined by (3.137) in units of eV.
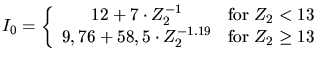 |
(3.137) |
The exponent 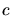 used for the interpolation around the stopping power maximum
allows to determine the height of the maximum of the total stopping power
used for the interpolation around the stopping power maximum
allows to determine the height of the maximum of the total stopping power
 . Besides a modification of the law for the non-local stopping power also a
modification of the energy dependence of the ratio between local and the
non-local part (3.132) is suggested for higher ion energies.
. Besides a modification of the law for the non-local stopping power also a
modification of the energy dependence of the ratio between local and the
non-local part (3.132) is suggested for higher ion energies.
 |
(3.138) |
The major drawback of the empirical model is that many empirical parameters
have to be determined especially for crystalline materials and therefore a lot
of SIMS measurements are necessary to extend this model to new material
types. But according to [31] the accuracy of the empirical model is
better than the model based on just the local electron density as has been
demonstrated for the case of boron implantations in crystalline
silicon. Additionally it requires less computational effort, because just the
impact parameter related to a certain collision event has to be determined to be
able to calculate the electronic stopping power related to a single collision
event.
The determination of the impact parameter requires no additional computational
effort, because it is also used to model the nuclear stopping power process. In
contrast the calculation of the local electron density along the flight path of
the ion is a very computational intensive task. Additionally, a numerical
integration of the electronic stopping power has to be performed in the local
electron density model, because the electron density varies significantly when
the ion passes an atom of the target.


 Previous: 3.3.3.2 Effective Charge of
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.4 Thermal Lattice Vibration
Previous: 3.3.3.2 Effective Charge of
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.4 Thermal Lattice Vibration
A. Hoessiger: Simulation of Ion Implantation for ULSI Technology
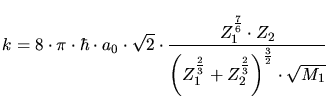
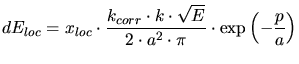
![]() for low ion velocities. A velocity of
for low ion velocities. A velocity of
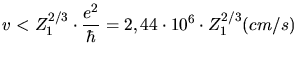
![]() and a stopping formula
derived by Bethe and Bloch
and a stopping formula
derived by Bethe and Bloch ![]() [1], [4],
[6], [39], which is valid for high ion energies, is
suggested in [75].
[1], [4],
[6], [39], which is valid for high ion energies, is
suggested in [75].
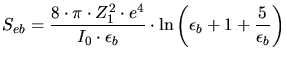
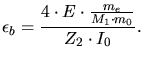
![]() used for the interpolation around the stopping power maximum
allows to determine the height of the maximum of the total stopping power
used for the interpolation around the stopping power maximum
allows to determine the height of the maximum of the total stopping power
![]() . Besides a modification of the law for the non-local stopping power also a
modification of the energy dependence of the ratio between local and the
non-local part (3.132) is suggested for higher ion energies.
. Besides a modification of the law for the non-local stopping power also a
modification of the energy dependence of the ratio between local and the
non-local part (3.132) is suggested for higher ion energies.

![]()
![]()
![]()
![]() Previous: 3.3.3.2 Effective Charge of
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.4 Thermal Lattice Vibration
Previous: 3.3.3.2 Effective Charge of
Up: 3.3.3 Electronic Stopping Process
Next: 3.3.4 Thermal Lattice Vibration