 |
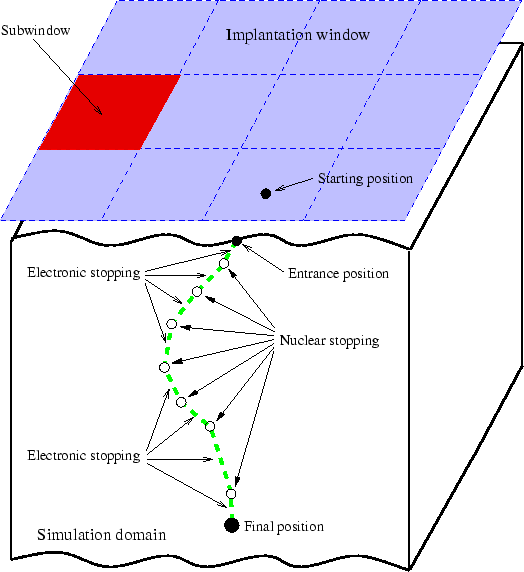
When the trajectory of an ion is calculated first the initial conditions are determined. Within the implantation window the starting position of an ion is selected randomly considering that the starting positions of all ions have to be equally distributed within the implantation window.
But instead of selecting the staring positions completely randomly a special procedure is applied. First the implantation window is split into rectangular sub-windows (Fig. 4.3). Then, for the selection of the starting positions of successive ions, a repeating scan over all sub-windows is performed and one ion is started from within each sub-window. The position of the ion inside the sub-window is determined randomly.
Even though this procedure does not seem to be necessary, the major advantage will be clarified in Sec. 4.6.3 where a parallelization strategy for the simulator is presented. By using this procedure the performance gain due to parallelization can be increased because this procedure avoids a random accumulation of successive starting positions within a small area of the implantation window. Another advantage is that using this procedure allows to define a time step for a transient simulation in a very convenient way, which is also necessary for a parallelization. One time step corresponds to one scan over all sub-windows. Except if the total number of simulated ions is very high (significantly higher than the number of sub-windows). In that case several scans over all sub-windows are performed during one time step, because the performance of the parallelization method increases by increasing the number of ions that are simulated per time step (Sec. 4.6.3).
The initial momentum of the ion is determined by the implantation conditions
described by the energy, the tilt and the twist angle. Additionally a
divergence ![]() of the ion beam can be specified. Thereby a random vector
with the polar angles
of the ion beam can be specified. Thereby a random vector
with the polar angles
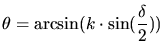 |
(4.1) |
| (4.2) |
Concerning the rotation angle, the simulator assumes that the rotation
angle 0
![]() is parallel to the x-axis when performing a three-dimensional
simulation, which means according to the definition of the rotation
(Sec. 2.2.4) that the y-axis is parallel to the primary flat of
the wafer. In case of a two-dimensional simulation it is assumed that the
simulated cut is parallel to the primary flat (equivalent to the y-axis of a
three-dimensional simulation).
is parallel to the x-axis when performing a three-dimensional
simulation, which means according to the definition of the rotation
(Sec. 2.2.4) that the y-axis is parallel to the primary flat of
the wafer. In case of a two-dimensional simulation it is assumed that the
simulated cut is parallel to the primary flat (equivalent to the y-axis of a
three-dimensional simulation).
![]()
![]()
![]()
![]() Previous: 4.2 Implantation Window
Up: 4. Monte-Carlo Simulation with
Next: 4.4 Trajectory Calculation
Previous: 4.2 Implantation Window
Up: 4. Monte-Carlo Simulation with
Next: 4.4 Trajectory Calculation