4.6.2 Trajectory-Reuse Method

In contrast to the Trajectory-Split method the Trajectory-Reuse method neither increases nor decreases the number of trajectories, but significantly reduces the average calculation time for one trajectory. The idea is to make use of the fact that several areas of the simulation domain are identical if just a small slice of the simulation domain around a single particle trajectory is looked at. Identical means that the material composition in such a small slice is identical to the material composition in a slice cut out of the simulation domain somewhere else. For instance the field oxide covers a large part of the simulation domain when simulating the implantation into a three-dimensional MOS-transistor structure and the shape of this field oxide only changes in the vicinity of the active area, while it has an almost planar surface and a constant thickness everywhere else.

The identical regions also behave identical with respect to the trajectory calculation it is therefore possible to calculate a trajectory just once and to copy it to other identical areas. This method can be interpreted as performing one-dimensional simulations and spreading them over a higher dimensional simulation domain as far as possible.

In the sense of trajectory calculation two regions are identical if all properties that have an influence on the motion of a particle are equal along the complete trajectory. In case of amorphous materials the material density and composition are considered while in case of crystalline materials also the damage distribution influences the trajectory calculation. Therefore the Trajectory-Reuse method can only be applied to amorphous materials, because the probability for identifying regions with an identical damage distribution along the particle trajectory is very low.

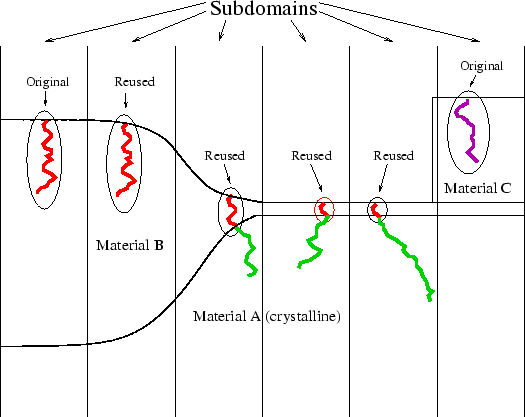
Fig. 4.20 illustrates how the Trajectory-Reuse method works.

Figure 4.20: Illustration of the functionality of the Trajectory-Reuse method.

As mentioned in Sec. 4.3 the implantation window is subdivided into several sub-windows and successively one ion is started from within each of these sub-windows during one scan. By the Trajectory-Reuse method not all trajectories for these ions are calculated rigorously. After calculating the first ion trajectory it is split into sub-trajectories, one for each amorphous material the particle moves through and these sub-trajectories are stored. The parts of the trajectory in crystalline materials are neglected. When the next ion is calculated the list of stored sub-trajectories is searched for an appropriate trajectory to be copied. The target material of the stored trajectory must be identical to the entrance material of the ion and the ion energy must be within the energy interval lost along the stored trajectory. If no suitable trajectory is in the stored list a new trajectory is calculated and new sub-trajectories are added to the list.

If a trajectory could be identified as suitable for copying it is adapted to the initial conditions of the ion. A collision event whose energy is closest to the initial energy of the ion is selected from the stored trajectory and the trajectory is transformed in a way that the position near the collision event with an appropriate energy equals the entrance point of the ion and that the momentum after the collision event equals the initial momentum of the ion. The whole procedure of selecting and transforming a stored trajectory is illustrated in Fig. 4.21. Worth mentioning is that a trajectory is only copied if the initial ion energy is within an energy interval corresponding to an electronic stopping process as shown in Fig. 4.21, to avoid an overestimation of recoiling processes which cover large intervals in the energy loss diagram.

Figure 4.21: Schematic description of the trajectory copying method.

The speedup due to the Trajectory-Reuse method is the higher the larger the number of sub-windows. Therefore it significantly increases especially the performance of three-dimensional simulations.