A well established model for thermal oxide growth has been proposed by Deal and Grove [51] in the middle of the 60's and because of its simplicity it is still applied frequently. One reason for this simplicity is that the whole physics of the oxidation process is contained in two so-called Deal-Grove parameters, which must be extracted from experiments. Furthermore, it is assumed that the structure is one-dimensional. Therefore, the model can only be applied to oxide films grown on plane substrates.
(1) It is transported from the bulk of the oxidizing gas to the outer surface of oxide, where it is adsorbed.
(2) It is transported across the oxide film towards silicon.
(3) It reacts at the interface with silicon and form a new layer of SiO![]() .
.
Each of these steps can be described as independent flux equation. The adsorption of oxidants is written as
| (2.8) |
It was found experimentally that wide changes in gas flow rates in the oxidation furnaces, changes in the spacing between wafers on the carrier in the furnace, and a change in wafer orientation (standing up or lying down) cause only little difference in oxidation rates. These results imply that ![]() is very large, or that only a small difference between
is very large, or that only a small difference between ![]() and
and ![]() is required to provide the necessary oxidant flux.
is required to provide the necessary oxidant flux.
![]() is also the solubility limit in the oxide, which is assumed to be related to the partial pressure
is also the solubility limit in the oxide, which is assumed to be related to the partial pressure ![]() of the oxidant in the gas atmosphere by Henry's law
of the oxidant in the gas atmosphere by Henry's law
The flux ![]() represents the diffusion of the oxidants through the oxide layer to the Si-SiO
represents the diffusion of the oxidants through the oxide layer to the Si-SiO![]() -interface, which can be expressed as
-interface, which can be expressed as
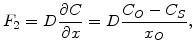 |
(2.10) |
The third part of the oxidation process is the flux of oxidants consumed by the oxidation reaction at the oxide-silicon interface given by
| (2.11) |
Deal and Grove assumed that in the steady state condition these three fluxes are equal, which allows to express them as
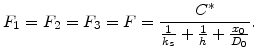 |
(2.12) |
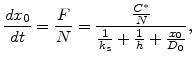 |
(2.13) |
The differential equation can be simplified as
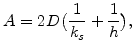 |
(2.15) |
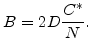 |
(2.16) |
In order to get an analytical relationship between oxide thickness ![]() and oxidation time
and oxidation time ![]() the first order differential equation (2.14) must be solved. For this purpose in the first step (2.14) can be rewritten in the form
the first order differential equation (2.14) must be solved. For this purpose in the first step (2.14) can be rewritten in the form
At first with (2.18) the oxidation time for a specific desired oxide thickness can be estimated by
On the other side solving the quadratic equation (2.18) in regard of x![]() leads to the following explicit expression for the oxide thickness in terms of oxidation time:
leads to the following explicit expression for the oxide thickness in terms of oxidation time:
The formulas (2.44) and (2.20) are a real strength of the Deal-Grove model, because the oxide thickness for any oxidation time or the needed time for a specific thickness can be determined in an uncomplicated and fast way. Of course the thickness can be only estimated in one direction on planar structures, but in practice this fast approach is indeed helpful.
It is interesting to examine two limiting forms of the linear-parabolic relationship (2.44). One limiting case occurs for long oxidation times when ![]() and
and
![]()
The rate constants ![]() and
and ![]() are also termed as Deal-Grove-parameters. In most publications which use the Deal-Grove model the oxide growth is described with
are also termed as Deal-Grove-parameters. In most publications which use the Deal-Grove model the oxide growth is described with ![]() and
and ![]() . The parameters
. The parameters ![]() and
and ![]() are normally determined experimentally by extracting them from growth data. The reason for taking this approach is simply that all parameters in (2.23) and (2.25) are not known.
are normally determined experimentally by extracting them from growth data. The reason for taking this approach is simply that all parameters in (2.23) and (2.25) are not known. ![]() in particular contains a lot of hidden physics associated with the interface reaction.
in particular contains a lot of hidden physics associated with the interface reaction.
In order to model the corresponding growth rate for different temperatures, the values for ![]() and
and ![]() must change with temperature. As explained in Section 2.4.2, the oxidation rate increases with higher temperature, and so the values of
must change with temperature. As explained in Section 2.4.2, the oxidation rate increases with higher temperature, and so the values of ![]() and
and ![]() must also increase. It was found experimentally that both
must also increase. It was found experimentally that both ![]() and
and ![]() are well described by Arrhenius expressions of the form
are well described by Arrhenius expressions of the form
| Ambient | ||
| Dry O |
|
|
| Wet H |
|
|
For the parabolic rate constant ![]() the activation energy
the activation energy ![]() is quite different for O
is quite different for O![]() and H
and H![]() O ambients. (2.23) suggests that the physical mechanism responsible for
O ambients. (2.23) suggests that the physical mechanism responsible for ![]() might be the oxidant diffusion through SiO
might be the oxidant diffusion through SiO![]() , because
, because ![]() is a constant and
is a constant and ![]() is not expected to increase exponentially with temperature. In fact, independent measurements of the diffusion coefficients of O
is not expected to increase exponentially with temperature. In fact, independent measurements of the diffusion coefficients of O![]() and H
and H![]() O in SiO
O in SiO![]() show that these parameters vary with temperature in the same way as (2.26) and with
show that these parameters vary with temperature in the same way as (2.26) and with ![]() values close to those shown in Table 2.2. The clear implication is that
values close to those shown in Table 2.2. The clear implication is that ![]() in the linear parabolic model really represents the oxidant diffusion process.
in the linear parabolic model really represents the oxidant diffusion process.
The ![]() values for
values for ![]() in the table are all quite close to 2 eV. (2.25) suggests that the physical origin of
in the table are all quite close to 2 eV. (2.25) suggests that the physical origin of ![]() is likely connected with the interface reaction rate
is likely connected with the interface reaction rate ![]() . Traditionally, the 2 eV activation energy has been associated with the Si-O bound formation process because of measurements by Pauling [52] that suggested that the Si-O bond energy was in the correct range to explain the
. Traditionally, the 2 eV activation energy has been associated with the Si-O bound formation process because of measurements by Pauling [52] that suggested that the Si-O bond energy was in the correct range to explain the ![]() values. However, the interface reaction is very complex and it is likely that other effects also affect the experimental
values. However, the interface reaction is very complex and it is likely that other effects also affect the experimental ![]() values. An additional observation supports the idea that it is somehow associated with the silicon substrate which determines
values. An additional observation supports the idea that it is somehow associated with the silicon substrate which determines ![]() , because
, because ![]() is essentially independent of the oxidation ambient. It is also essentially independent of the substrate crystal orientation, which suggests that
is essentially independent of the oxidation ambient. It is also essentially independent of the substrate crystal orientation, which suggests that ![]() represents a fundamental part of the oxidation process, not something only associated with the substrate.
represents a fundamental part of the oxidation process, not something only associated with the substrate.
The linear parabolic model predicts that the oxide growth rate should be directly proportional to the oxidant pressure as shown in (2.9). If Henry's law [53] holds and the concentration of oxidants on the gas/SiO![]() interface
interface ![]() is proportional to the pressure
is proportional to the pressure ![]() , then both
, then both ![]() and
and ![]() are proportional to
are proportional to ![]() from (2.23) and (2.25), and the oxide growth rate should therefore be proportional to
from (2.23) and (2.25), and the oxide growth rate should therefore be proportional to ![]() .
.
Experimental measurements have shown that for wet oxidation this prediction is correct, and for H![]() O ambients the pressure dependence of the parabolic and linear rate constants are [36]
O ambients the pressure dependence of the parabolic and linear rate constants are [36]
If ![]() is not linearly proportional to
is not linearly proportional to ![]() ,
, ![]() from (2.25) must depend on
from (2.25) must depend on ![]() in a non-linear fashion. Considering the pressure dependence of
in a non-linear fashion. Considering the pressure dependence of ![]() and
and ![]() above, the chemical surface reaction must depend on pressure in the way
above, the chemical surface reaction must depend on pressure in the way
![]() .
.
Even before the development of the Deal-Grove model, it has been observed that crystal orientation affects the oxidation rate [39]. The crystal effects can be incorporated in the following way: Except perhaps in the region very near the Si/SiO![]() interface, the oxide grows on silicon in an amorphous way. So it does not incorporate any information about the underlying silicon crystal structure. Therefore, the parabolic rate constant B should not be orientation dependent, since B represents the oxidant diffusion through the SiO
interface, the oxide grows on silicon in an amorphous way. So it does not incorporate any information about the underlying silicon crystal structure. Therefore, the parabolic rate constant B should not be orientation dependent, since B represents the oxidant diffusion through the SiO![]() . If the oxide structure is unrelated to the underlying substrate, there should be no crystal orientation effect on B. In fact it was found experimentally by extracting growth data [38], that in context of the model there is no crystal effect on the rate constant B. The B values are the same for all orientations.
. If the oxide structure is unrelated to the underlying substrate, there should be no crystal orientation effect on B. In fact it was found experimentally by extracting growth data [38], that in context of the model there is no crystal effect on the rate constant B. The B values are the same for all orientations.
On the other hand B/A should be orientation dependent, because it involves the reaction at the Si/SiO![]() interface. This reaction surely involves silicon atoms and should be affected by the number of available reaction sites. It was found experimentally [38],
that there are two extremes of the linear rate constant B/A. The minimum was found for (100) oriented silicon whereas the maximum is at (111) orientation, and all other orientation are normally between these two extremes. In the context of the model the orientation effect must be incorporated for the rate constant B/A in the following way [38]:
interface. This reaction surely involves silicon atoms and should be affected by the number of available reaction sites. It was found experimentally [38],
that there are two extremes of the linear rate constant B/A. The minimum was found for (100) oriented silicon whereas the maximum is at (111) orientation, and all other orientation are normally between these two extremes. In the context of the model the orientation effect must be incorporated for the rate constant B/A in the following way [38]:
It has been observed in many experiments that there is a rapid and non-linear oxide growth in the initial stage of dry oxidation [54], as presented in Fig. 2.18. One weakness of the model is the impossibility to predict the initial stage of the oxidation growth. As shown in Fig. 2.18, even with the best fit, the approximately first 30 nm of the oxide thickness can not be forecasted with the linear parabolic model, because the oxide growth is fast and non-linear but the model offers only a linear fit for such thin thicknesses [55] .