


Next: 3. Advanced Oxidation Model
Up: 2. Physics of Thermal
Previous: 2.6 The Deal-Grove Model
Subsections
As described in the Section 2.6.6 the Deal-Grove model can not satisfy the so-called thin film oxidation. It should be taken into account that in the middle of the 60's, when Deal and Grove developed their model, oxide thicknesses under 30 nm were not fabricated in the semiconductor technology. Hence, there was no need to predict or simulate the growth for such thin oxide films. But with shrinking device geometry also the oxide thickness is decreasing. Hence, sometime in the 80's, MOS gates with thin thicknesses were grown and so the problem became important. In order to handle also thin film oxditation, in this time Massoud and other people, reengineered the Deal-Grove concept [56]. The yielded model is most suitable for thin oxide films, but it should be mentioned that it also works well for other oxide thicknesses. The price for this common validity is the higher complexity of this model.
It was found that the SiO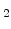 growth rate in the thin regime for a wide variety of experimental conditions can be expressed as [56]
growth rate in the thin regime for a wide variety of experimental conditions can be expressed as [56]
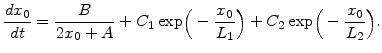 |
(2.33) |
The first term on the right side of (2.33) is the linear-parabolic term where 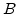 and
and 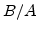 are the parabolic and linear rate constants, respectively, as defined by Deal and Grove, but their values in the Massoud model are completely different [57]. In Arrhenius-expression the rate constants can be written in the form
are the parabolic and linear rate constants, respectively, as defined by Deal and Grove, but their values in the Massoud model are completely different [57]. In Arrhenius-expression the rate constants can be written in the form
The values for the pre-exponential constants 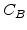 ,
, 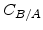 and the activation energies
and the activation energies 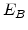 ,
, 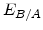 for different crystal orientations are listed in Table 2.3. In this model it is adverse that
for different crystal orientations are listed in Table 2.3. In this model it is adverse that 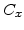 and
and 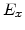 are not valid for the whole temperature range and so
are not valid for the whole temperature range and so 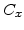 and
and 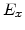 differ from temperatures less and more than 1000
differ from temperatures less and more than 1000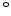 C.
C.
Table 2.3:
Pre-exponential constants and activation energies for 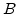 and
and 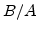 [57].
[57].
| Temperature Range |
T < 1000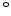 C C |
T > 1000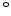 C C |
| Crystal Orientation |
|
(100) |
(111) |
(110) |
(100) |
(111) |
 |
[nm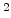 /min] /min] |
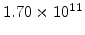 |
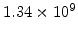 |
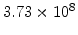 |
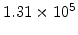 |
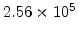 |
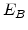 |
[eV] |
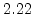 |
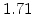 |
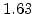 |
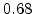 |
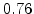 |
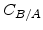 |
[nm/min] |
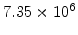 |
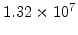 |
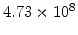 |
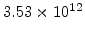 |
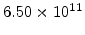 |
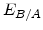 |
[eV] |
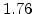 |
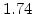 |
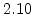 |
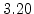 |
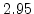 |
In (2.33) the two exponential terms represent the rate enhancement in the thin regime. They are defined in terms of pre-exponential constants 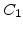 and
and 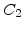 and characteristic lengths
and characteristic lengths 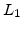 and
and 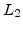 . The first decaying exponential has a characteristic lengths
. The first decaying exponential has a characteristic lengths 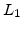 in the order of 1nm, it is nonzero for the first 5nm of oxide growth, and vanishes for oxides thicker than 5nm. The second decaying exponential has a
characteristic lengths
in the order of 1nm, it is nonzero for the first 5nm of oxide growth, and vanishes for oxides thicker than 5nm. The second decaying exponential has a
characteristic lengths 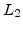 in the order of 7nm and it is present from the onset of oxidation to an oxide thickness of about 25nm, where it decays to zero and the growth becomes pure linear-parabolic.
in the order of 7nm and it is present from the onset of oxidation to an oxide thickness of about 25nm, where it decays to zero and the growth becomes pure linear-parabolic.
Another formulation of (2.33), where the two terms which represent the rate enhancement in the thin regime are decaying exponentially with time, can be expressed as [58]
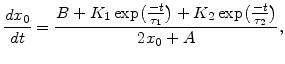 |
(2.36) |
where all four parameters 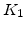 ,
, 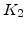 ,
, 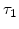 and
and 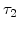 were fitted to an Arrhenius-type expression
were fitted to an Arrhenius-type expression
The pre-exponential constants and activation energies in the above expressions (2.37)-(2.40) for different crystal orientations and dry oxidation in the temperature range form 800-1000 C are listed in Table 2.4.
C are listed in Table 2.4.
Table 2.4:
Arrhenius-expression parameters for the pre-exponential constants 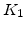 and
and 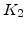 , and the time constants
, and the time constants 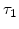 and
and 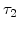 in the 800 - 1000
in the 800 - 1000  C range [58].
C range [58].
| Crystal Orientation |
|
(100) |
(111) |
(110) |
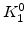 |
[nm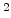 /min] /min] |
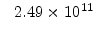 |
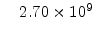 |
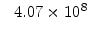 |
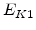 |
[eV] |
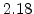 |
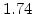 |
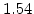 |
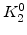 |
[nm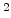 /min] /min] |
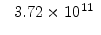 |
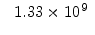 |
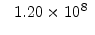 |
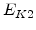 |
[eV] |
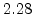 |
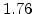 |
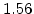 |
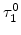 |
[min] |
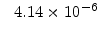 |
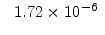 |
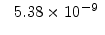 |
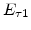 |
[eV] |
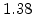 |
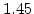 |
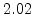 |
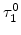 |
[min] |
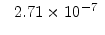 |
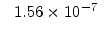 |
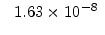 |
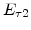 |
[eV] |
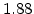 |
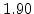 |
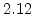 |
As already mentioned in Section 2.6.2, it would be convenient to have an analytical expression for the oxide thickness 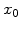 . For this purpose (2.36) is rewritten as
. For this purpose (2.36) is rewritten as
![$\displaystyle (2x_0+A)dx_0=\Big[ B+K_1 \mathrm{exp}\Big(-\frac{t}{\tau_1}\Big)+K_2 \mathrm{exp}\Big(-\frac{t}{\tau_2}\Big)\Big]dt.$](img217.png) |
(2.41) |
Integration of (2.41), from time 0 where the native oxide thickness is x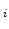 to an oxidation time t where the oxide thickness x
to an oxidation time t where the oxide thickness x results in [58]
results in [58]
![$\displaystyle x_0^2 +Ax_0=Bt+M_1\Big[ 1-\mathrm{exp}\Big(-\frac{t}{\tau_1}\Big)\Big]+M_2\Big[ 1-\mathrm{exp}\Big(-\frac{t}{\tau_2}\Big)\Big]+M_0$](img219.png) |
(2.42) |
with the substitutions
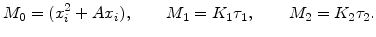 |
(2.43) |
The equation (2.42) is quadratic and can be solved obtaining an analytic expression for the oxide thickness as a function of the oxidation time of the form
![$\displaystyle x_0=\sqrt{\Big(\frac{A}{2}\Big)^2 +Bt+M_1\Big[ 1-\mathrm{exp}\Big...
...)\Big]+M_2\Big[ 1-\mathrm{exp}\Big(-\frac{t}{\tau_2}\Big)\Big]+M_0}-\frac{A}{2}$](img221.png) |
(2.44) |
This relationship describes the oxide growth in dry oxygen from the onset oxidation with an smaller than 1-2% compared to the measured data. An example in Fig. 2.19 shows the growth in thin regime for (100) oriented silicon in temperature range 900-1000 C. The oxide thicknesses were calculated by (2.42) with the parameters from Table 2.3 and 2.4.
C. The oxide thicknesses were calculated by (2.42) with the parameters from Table 2.3 and 2.4.
Figure 2.19:
Oxide thickness versus oxidation time for (110) oriented silicon in dry oxygen at 900  C, 950
C, 950  C, and 1000
C, and 1000  C.
C.
|
|



Next: 3. Advanced Oxidation Model
Up: 2. Physics of Thermal
Previous: 2.6 The Deal-Grove Model
Ch. Hollauer: Modeling of Thermal Oxidation and Stress Effects
![]() growth rate in the thin regime for a wide variety of experimental conditions can be expressed as [56]
growth rate in the thin regime for a wide variety of experimental conditions can be expressed as [56]
![]() . For this purpose (2.36) is rewritten as
. For this purpose (2.36) is rewritten as
![\includegraphics[width=0.75\linewidth,bb=29 52 716 528, clip]{curv/mass/drymas}](img222.png)