3.3 Model Overview

The whole advanced oxidation model is based on a few main equations. The first one describes the oxidant diffusion

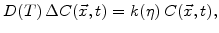$$D(T) \Delta C(\vec{x},t) = k(\eta) C(\vec{x},t),$$ (3.38)

and the next equation treats the dynamics of 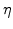$\eta$ with

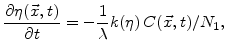$$\frac{\partial \eta(\vec{x},t)} {\partial t} = - \frac{1}{\lambda} k(\eta) C(\vec{x},t)/N_1,$$ (3.39)

as described in Section 3.2.1 and Section 3.2.2, respectively.

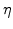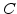Because of the diffuse interface concept the volume increase of the generating oxide occurs only successively and not abruptly. As explained in Section 3.2.3, the volume increase of the oxidized material is calculated with the $\eta$ and $C$ values. After a time 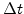$\Delta t$ the normalized additional volume is determined by

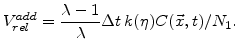$$V^{add}_{rel} = \frac{\lambda - 1}{\lambda}\Delta t k(\eta) C(\vec{x},t)/N_1.$$ (3.40)

The normalized additional volume directly loads the mechanical problem

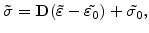$$\tilde{\sigma} = \mathbf{D} (\tilde{\varepsilon} - \tilde{\varepsilon_0}) + \tilde{\sigma_0},$$ (3.41)

because the principal axis components of the residual strain tensor 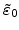$\tilde\varepsilon_0$ are linearly proportional to 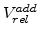$V^{add}_{rel}$ in the form

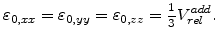$$\varepsilon_{0,xx}=\varepsilon_{0,yy}=\varepsilon_{0,zz}=\frac{{}_1}{{}^3}V^{add}_{rel}.$$ (3.42)

The introduced so-called effective shear modulus 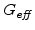$G_\mathit{eff}$ in $\mathbf{D}$ (see Section 3.2.5.2) can handle elastic and visco-elastic materials.