


Next: 3.3 Model Overview
Up: 3. Advanced Oxidation Model
Previous: 3.1 The Diffuse Interface
Subsections
From the mathematical point of view the whole oxidation process can be described by a coupled system of partial differential equations, one for the diffusion of oxidants through SiO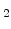 , the second for the conversion of Si into SiO
, the second for the conversion of Si into SiO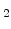 at the interface, and a third for the mechanical problem of the complete oxidized structure.
at the interface, and a third for the mechanical problem of the complete oxidized structure.
3.2.1 Oxidant Diffusion
The diffusion of oxidants in the domains 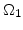 ,
, 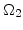 , and
, and 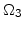 according to Fig. 3.1 is described by
according to Fig. 3.1 is described by
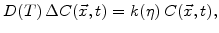 |
(3.2) |
where
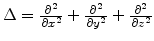 is the Laplace operator,
is the Laplace operator,
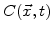 is the oxidant concentration in the material, and
is the oxidant concentration in the material, and 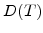 is the temperature dependent low stress diffusion coefficient.
is the temperature dependent low stress diffusion coefficient.
The boundary conditions for the diffusion equation (3.2) are
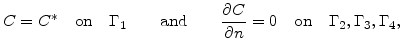 |
(3.3) |
where 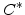 is the oxidant concentration in the gas atmosphere.
is the oxidant concentration in the gas atmosphere.
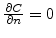 is a Neumann boundary condition, which means that there does not exist an oxidant flow through these boundaries.
is a Neumann boundary condition, which means that there does not exist an oxidant flow through these boundaries.
In (3.2) 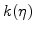 is the strength of a spatial sink and not just a reaction coefficient at a sharp interface [67].
is the strength of a spatial sink and not just a reaction coefficient at a sharp interface [67].
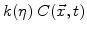 defines how many particles of oxygen per unit volume are transformed in a unit time interval to oxide.
defines how many particles of oxygen per unit volume are transformed in a unit time interval to oxide. 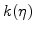 is defined to be linearly proportional to
is defined to be linearly proportional to
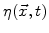
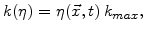 |
(3.4) |
where 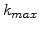 is the maximal possible strength of the sink.
is the maximal possible strength of the sink.
Figure 3.1:
Schematic domains and boundaries.
|
|
3.2.2 Dynamics of
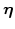
Because of the chemical reaction which consumes silicon, the normalized silicon concentration 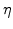 is changed. In a test volume
is changed. In a test volume
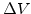 , where is assumed that the oxidant concentration C is constant during a time interval
, where is assumed that the oxidant concentration C is constant during a time interval 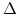
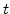 there are
there are
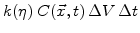 particles of oxygen which react with
particles of oxygen which react with
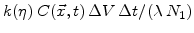 unit volumes of silicon. By this process the silicon concentration is reduced.
unit volumes of silicon. By this process the silicon concentration is reduced.
The dynamics of 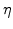 can be described by [67]
can be described by [67]
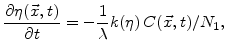 |
(3.5) |
where 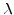 is the volume expansion factor (=2.25) for the reaction from Si
to SiO
is the volume expansion factor (=2.25) for the reaction from Si
to SiO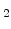 , and
, and 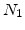 is the number of oxidant molecules incorporated into
one unit volume of SiO
is the number of oxidant molecules incorporated into
one unit volume of SiO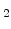 .
.
In this model the dynamics of 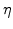 is equivalent with the movement of the sharp Si/SiO
is equivalent with the movement of the sharp Si/SiO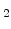 interface in the standard model, because
interface in the standard model, because 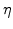 defines the silicon and oxide areas. The only difference is that here a diffuse interface (Fig. 3.1) moves, where is a mixture of silicon and oxide.
defines the silicon and oxide areas. The only difference is that here a diffuse interface (Fig. 3.1) moves, where is a mixture of silicon and oxide.
3.2.3 Volume Expansion of the New Oxide
Because of the much lower density of oxide compared with silicon, the conversion from Si to SiO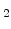 leads to a significant volume increase of the new oxide.
In the advanced model the conversion is not performed instantaneously, it needs some finite time. The fraction of SiO
leads to a significant volume increase of the new oxide.
In the advanced model the conversion is not performed instantaneously, it needs some finite time. The fraction of SiO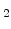 in a small volume
in a small volume 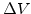 is expressed by the
is expressed by the 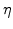 value. The new generated oxide in the reaction layer is described by the change of
value. The new generated oxide in the reaction layer is described by the change of 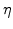 . For a time period
. For a time period 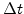 the
the 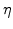 -value and the silicon fraction decreases with
-value and the silicon fraction decreases with
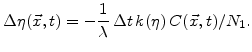 |
(3.6) |
The additional volume in a test volume 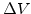 is given by
is given by
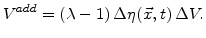 |
(3.7) |
Because the maximal volume increase of the oxide is limited to 1.25 times of the volume of original silicon, 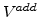 in (3.7) must be scaled with (
in (3.7) must be scaled with (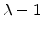 ).
).
The normalized additional volume with (3.6) and (3.7) after a time 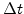 is
is
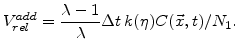 |
(3.8) |
An important aspect of (3.8) is that the sum of
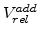 over all time steps can not be more than 125%, which is the maximal volume increase of the material during oxidation.
over all time steps can not be more than 125%, which is the maximal volume increase of the material during oxidation.
3.2.4 Diffusion Coefficient and Reaction Layer
In contrast to the standard models, where the diffusion coefficient 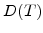 is automatically included in the parabolic rate constant B, in the advanced model
is automatically included in the parabolic rate constant B, in the advanced model 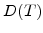 must be determined separately for the specific temperature and oxidant species. The most interesting oxidant species come from dry and wet oxidation.
must be determined separately for the specific temperature and oxidant species. The most interesting oxidant species come from dry and wet oxidation.
In general the diffusion coefficient follows the expression
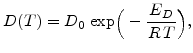 |
(3.9) |
where 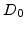 is a pre-exponential diffusion constant,
is a pre-exponential diffusion constant, 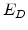 is the activation energy in [cal], T the temperature in [K], and
is the activation energy in [cal], T the temperature in [K], and 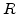 is the universal gas constant with
is the universal gas constant with 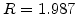 cal/(K
cal/(K mol).
mol).
For dry oxygen ambients the results of Norton [68] can be used, who found that the activation energy for diffusion of oxygen in vitreous silica is 27 kcal and the diffusion coefficient 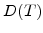 is 4.2
is 4.2
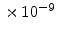 cm
cm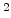 /sec (= 0.42
/sec (= 0.42 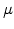 m
m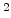 /sec) at a temperature of 950
/sec) at a temperature of 950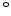 C. With these data it is possible to calculate
C. With these data it is possible to calculate 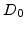 , and (3.9) can be written for dry oxidation in the form
, and (3.9) can be written for dry oxidation in the form
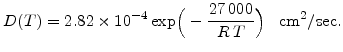 |
(3.10) |
For wet oxidation the results from Moulson and Roberts [69] are most suitable. They have investigated heated silica glass in water vapour between 600 and 1200 C and found the temperature dependent diffusion coefficient
C and found the temperature dependent diffusion coefficient
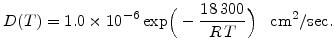 |
(3.11) |
In the advanced model the reaction layer has a spatial finite width d
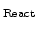 , which can vary. This width is mainly determined by the value of
, which can vary. This width is mainly determined by the value of 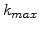 . The bigger
. The bigger 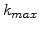 , the steeper the concentration decay and the thinner the reaction layer.
Therefore, d
, the steeper the concentration decay and the thinner the reaction layer.
Therefore, d
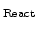 is inverse proportional to
is inverse proportional to 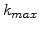 and so the width can be controlled by
and so the width can be controlled by
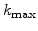 . This means that a small value of
. This means that a small value of 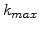 (e.g.
(e.g.
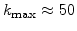 ) leads to a wide reaction layer (e.g d
) leads to a wide reaction layer (e.g d
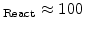 nm) and a big value of
nm) and a big value of 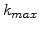 (e.g.
(e.g.
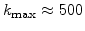 ) leads to a small reaction layer (e.g d
) leads to a small reaction layer (e.g d
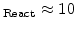 nm).
nm).
The layer width is an important and necessary fact, because the thickness of the reaction layer must be much smaller than the thickness of the oxidized structure or the final oxide thickness. In order to apply this model also for dry or thin film oxidation with a few nm thickness, wide reaction layers are unusable.
Another interesting aspect of this model is the value of the diffusion coefficient
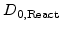 in the reaction layer. In the standard model with a sharp interface the oxidants diffuse with the same
in the reaction layer. In the standard model with a sharp interface the oxidants diffuse with the same 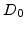 through the oxide to the Si/SiO
through the oxide to the Si/SiO -interface where they react. This means that in the standard model no oxidants diffuse into silicon and a normalized coefficient
-interface where they react. This means that in the standard model no oxidants diffuse into silicon and a normalized coefficient
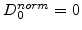 in the silicon and
in the silicon and
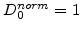 in the oxide are appropriate.
in the oxide are appropriate.
In the advanced model the oxidant diffusion must not stop at the beginning of the reaction layer, because there the oxidants are needed for the chemical reaction. On the other side the oxidant diffusion should stop at the end of the reaction layer and not continue into the silicon material. A good approach for this model is that the values of
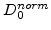 run down gradually from an approximate value of 1 near the oxide area to a value of 0 near the silicon area as schematically shown in Fig. 3.2.
run down gradually from an approximate value of 1 near the oxide area to a value of 0 near the silicon area as schematically shown in Fig. 3.2.
Since 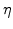 defines the domains of oxide, reaction layer as well as silicon, and during the oxidation process the reaction layer moves into the silicon domain,
defines the domains of oxide, reaction layer as well as silicon, and during the oxidation process the reaction layer moves into the silicon domain,
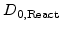 must be a function of
must be a function of 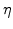 . Because the value of
. Because the value of
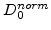 must be 1 in SiO
must be 1 in SiO , where
, where 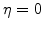 , and 0 in Si, where
, and 0 in Si, where 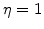 (see Fig. 3.2), the most plausible function for the diffusion coefficient in the reaction layer is
(see Fig. 3.2), the most plausible function for the diffusion coefficient in the reaction layer is
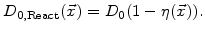 |
(3.12) |
Another simple but good working formulation for
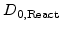 in the reaction layer was found with
in the reaction layer was found with
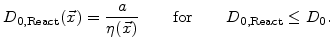 |
(3.13) |
Here 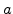 is a small constant and
is a small constant and
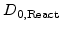 must be limited to
must be limited to 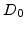 when
when
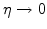 .
.
Figure 3.2:
Values of 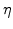 and D
and D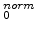 in the reaction layer.
in the reaction layer.
|
|
3.2.5 Mechanics
The chemical reaction of silicon and oxygen causes a volume increase of about 125%, which leads to significant displacements in the material. If this volume increase is only partially prevented, mechanical stress is built up in the materials. In order to calculate these displacements and stresses a mechanical modeling is needed.
In general, every three-dimensional mechanical problem can be described by the stress equilibrium relations [70]
During the oxidation process there are normally no external forces, because a volume increase caused by a chemical reaction, or a thermal expansion only lead to internal forces. Therefore, on the right-hand side of (3.14) the external forces are
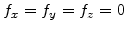 .
.
For linear elastic materials which are described by the Hook's law, the stress tensor
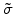 from (3.14) is given by
from (3.14) is given by
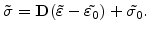 |
(3.15) |
Here
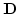 is the so-called material matrix. Furthermore,
is the so-called material matrix. Furthermore,
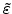 is the strain tensor,
is the strain tensor,
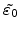 is the residual strain tensor, and
is the residual strain tensor, and
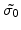 is the residual stress tensor.
is the residual stress tensor.
For constructing the material matrix
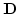 , the components of the stress tensor without residual stress and strain components can be expressed in Lame's form by [71]
, the components of the stress tensor without residual stress and strain components can be expressed in Lame's form by [71]
 |
(3.16) |
where
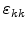 is the trace of the strain tensor
is the trace of the strain tensor
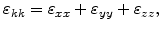 |
(3.17) |
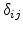 is the Kronecker symbol
is the Kronecker symbol
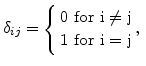 |
(3.18) |
and 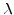 and
and 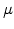 are the so-called Lame's constants
are the so-called Lame's constants
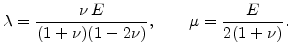 |
(3.19) |
Thereby 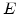 is the Young modulus and
is the Young modulus and 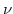 is the Poisson ratio. Note, the often used shear modulus
is the Poisson ratio. Note, the often used shear modulus 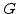 is identical with Lame's constant
is identical with Lame's constant 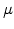 .
.
The strain tensor is
![$\displaystyle \tilde{\varepsilon}= \left[ \begin{array}{ccc} \varepsilon_{xx} &...
...\gamma_{zx} & \frac{1}{2}\gamma_{zy} & \varepsilon_{zz} \end{array} \right].$](img301.png) |
(3.20) |
The elements
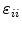 are the first derivatives of the displacements
are the first derivatives of the displacements 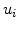 so that
so that
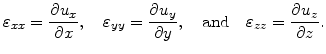 |
(3.21) |
The shear strain components
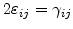 are given by [72]
are given by [72]
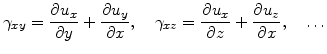 |
(3.22) |
If an isotropic material is assumed, the strain tensor is symmetric due to
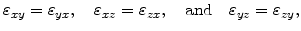 |
(3.23) |
which means that there are only six different values.
Assuming an isotropic material and after constructing
 with the help of (3.16), the stress tensor without residual stress, can be rewritten in the form
with the help of (3.16), the stress tensor without residual stress, can be rewritten in the form
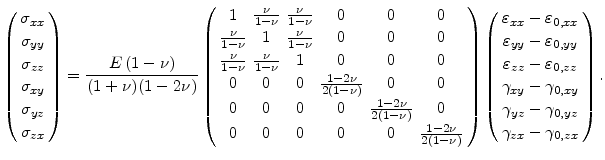 |
(3.24) |
3.2.5.2 Visco-Elastic Mechanical Model
The material behavior of oxide and nitride are more realistically described with a visco-elastic model [73,74], especially with a so-called Maxwell element (see Fig. 3.3), which consists of a spring and a dashpot in series. The characteristics of such a Maxwell element is that it takes the stress relaxation and the stress history into account. Also the actual stress is influenced from both, the strain and the strain rate, and, therefore, the stress is a function of time. The Maxwell element can be mathematically formulated with
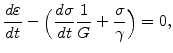 |
(3.25) |
where 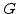 is the shear modulus and
is the shear modulus and 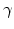 is the (shear) viscosity.
is the (shear) viscosity.
Figure 3.3:
Maxwell element: a spring and a dashpot in series.
|
|
The analytical solution of (3.25) for the temporal stress evolution as a function of the strain velocity is
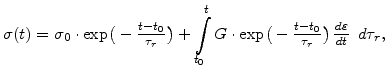 |
(3.26) |
where 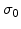 is the initial stress at time
is the initial stress at time 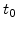 and
and 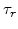 is the Maxwellian relaxation time constant
is the Maxwellian relaxation time constant
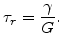 |
(3.27) |
In (3.26) the first term shows that the initial stress relaxes exponentially with time. The evaluation of the integral part leads to
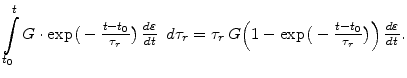 |
(3.28) |
The visco-elastic model is based on the idea that the dilatational components of the stress, which involve the volumetric expansion or compression, and the deviatoric components which only include the shape modification, can be decoupled [75]. For this purpose the material matrix
 from (3.24) can be split in a dilatation and a deviatoric part [76]
from (3.24) can be split in a dilatation and a deviatoric part [76]
![$\displaystyle \mathbf{D}=\mathbf{D}_{dil}+\mathbf{D}_{dev}= \left(H\left[ \begi...
...om{-}0 &\phantom{-}0 &\phantom{-}0 &\phantom{-}1 \end{array} \right] \right).$](img318.png) |
(3.29) |
Here  is the bulk modulus
is the bulk modulus
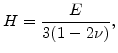 |
(3.30) |
and
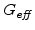 is the so-called effective shear modulus which is in the elastic case the same as the standard shear modulus
is the so-called effective shear modulus which is in the elastic case the same as the standard shear modulus
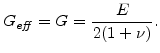 |
(3.31) |
In Maxwell's model the dilatation part is assumed purely elastic, while the deviatoric part is modeled by the Maxwell element.
In order to find an uncomplicated Maxwell formulation for the deviatoric part in (3.29), it can be assumed in (3.28) that for a short time period 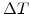 the strain velocity can be kept constant
the strain velocity can be kept constant
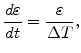 |
(3.32) |
so that (3.28) can be expressed in the form
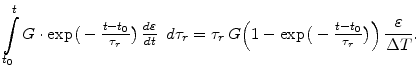 |
(3.33) |
So in the visco-elastic case
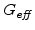 can be written in the form [77,78]
can be written in the form [77,78]
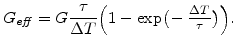 |
(3.34) |
This relationship shows that the Maxwell visco-elasticity can be expressed by an effective shear modulus
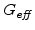 in the deviatoric part of the material matrix
in the deviatoric part of the material matrix
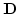 (3.24). This means that the only difference in the mechanical model between the elastic and visco-elastic case is the different
(3.24). This means that the only difference in the mechanical model between the elastic and visco-elastic case is the different
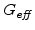 in the material matrix
in the material matrix
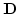 . So
. So
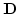 depends in the elastic case only on Young's modulus
depends in the elastic case only on Young's modulus 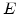 and the Poisson ratio
and the Poisson ratio
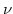 , and in the visco-elastic case additionally on the Maxwellian relaxation time
, and in the visco-elastic case additionally on the Maxwellian relaxation time 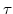 .
.
A very important aspect in the oxidation model is, how the volume increase during oxidation can be brought in relation with the mechanical problem. In three dimensions a volume expansion can be formulated with
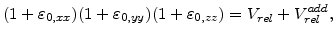 |
(3.35) |
where 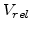 is the normalized volume before expansion and thus
is the normalized volume before expansion and thus 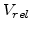 is always 1.
is always 1.
By assuming that the volume expansion and the strain is small, the strain terms
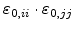 can be neglected (
can be neglected (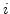 and
and 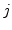 stands for
stands for 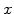 ,
, 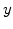 or
or 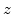 ), because they are much smaller than the terms
), because they are much smaller than the terms
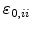 . Therefore, with the start volume
. Therefore, with the start volume 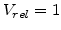 , (3.35) can be reduced to the form
, (3.35) can be reduced to the form
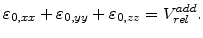 |
(3.36) |
The components
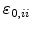 of the residual strain tensor
of the residual strain tensor
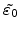 are linearly proportional to the normalized additional volume as calculated in (3.8)
are linearly proportional to the normalized additional volume as calculated in (3.8)
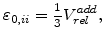 |
(3.37) |
which loads the mechanical problem (3.15) for calculating the displacements and stresses.



Next: 3.3 Model Overview
Up: 3. Advanced Oxidation Model
Previous: 3.1 The Diffuse Interface
Ch. Hollauer: Modeling of Thermal Oxidation and Stress Effects
![]() is changed. In a test volume
is changed. In a test volume
![]() , where is assumed that the oxidant concentration C is constant during a time interval
, where is assumed that the oxidant concentration C is constant during a time interval ![]()
![]() there are
there are
![]() particles of oxygen which react with
particles of oxygen which react with
![]() unit volumes of silicon. By this process the silicon concentration is reduced.
unit volumes of silicon. By this process the silicon concentration is reduced.
![]() can be described by [67]
can be described by [67]
![]() is equivalent with the movement of the sharp Si/SiO
is equivalent with the movement of the sharp Si/SiO![]() interface in the standard model, because
interface in the standard model, because ![]() defines the silicon and oxide areas. The only difference is that here a diffuse interface (Fig. 3.1) moves, where is a mixture of silicon and oxide.
defines the silicon and oxide areas. The only difference is that here a diffuse interface (Fig. 3.1) moves, where is a mixture of silicon and oxide.
![]() leads to a significant volume increase of the new oxide.
In the advanced model the conversion is not performed instantaneously, it needs some finite time. The fraction of SiO
leads to a significant volume increase of the new oxide.
In the advanced model the conversion is not performed instantaneously, it needs some finite time. The fraction of SiO![]() in a small volume
in a small volume ![]() is expressed by the
is expressed by the ![]() value. The new generated oxide in the reaction layer is described by the change of
value. The new generated oxide in the reaction layer is described by the change of ![]() . For a time period
. For a time period ![]() the
the ![]() -value and the silicon fraction decreases with
-value and the silicon fraction decreases with
![]() is
is
![]() is 4.2
is 4.2
![]() cm
cm![]() /sec (= 0.42
/sec (= 0.42 ![]() m
m![]() /sec) at a temperature of 950
/sec) at a temperature of 950![]() C. With these data it is possible to calculate
C. With these data it is possible to calculate ![]() , and (3.9) can be written for dry oxidation in the form
, and (3.9) can be written for dry oxidation in the form
![]() in the reaction layer. In the standard model with a sharp interface the oxidants diffuse with the same
in the reaction layer. In the standard model with a sharp interface the oxidants diffuse with the same ![]() through the oxide to the Si/SiO
through the oxide to the Si/SiO![]() -interface where they react. This means that in the standard model no oxidants diffuse into silicon and a normalized coefficient
-interface where they react. This means that in the standard model no oxidants diffuse into silicon and a normalized coefficient
![]() in the silicon and
in the silicon and
![]() in the oxide are appropriate.
in the oxide are appropriate.
![]() run down gradually from an approximate value of 1 near the oxide area to a value of 0 near the silicon area as schematically shown in Fig. 3.2.
run down gradually from an approximate value of 1 near the oxide area to a value of 0 near the silicon area as schematically shown in Fig. 3.2.
![]() defines the domains of oxide, reaction layer as well as silicon, and during the oxidation process the reaction layer moves into the silicon domain,
defines the domains of oxide, reaction layer as well as silicon, and during the oxidation process the reaction layer moves into the silicon domain,
![]() must be a function of
must be a function of ![]() . Because the value of
. Because the value of
![]() must be 1 in SiO
must be 1 in SiO![]() , where
, where ![]() , and 0 in Si, where
, and 0 in Si, where ![]() (see Fig. 3.2), the most plausible function for the diffusion coefficient in the reaction layer is
(see Fig. 3.2), the most plausible function for the diffusion coefficient in the reaction layer is
![]() from (3.14) is given by
from (3.14) is given by
![]() , the components of the stress tensor without residual stress and strain components can be expressed in Lame's form by [71]
, the components of the stress tensor without residual stress and strain components can be expressed in Lame's form by [71]
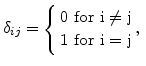
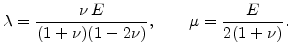
![$\displaystyle \tilde{\varepsilon}= \left[ \begin{array}{ccc} \varepsilon_{xx} &...
...\gamma_{zx} & \frac{1}{2}\gamma_{zy} & \varepsilon_{zz} \end{array} \right].$](img301.png)
![]() with the help of (3.16), the stress tensor without residual stress, can be rewritten in the form
with the help of (3.16), the stress tensor without residual stress, can be rewritten in the form
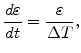
![]() can be neglected (
can be neglected (![]() and
and ![]() stands for
stands for ![]() ,
, ![]() or
or ![]() ), because they are much smaller than the terms
), because they are much smaller than the terms
![]() . Therefore, with the start volume
. Therefore, with the start volume ![]() , (3.35) can be reduced to the form
, (3.35) can be reduced to the form