The force which is generated by grain island impingement is [145]
The goal of the modeling is to express the previous described microscopic stress phenomena with a macroscopic stress formulation for the respective source.
![]() Coalescence of Grain Boundaries:
Coalescence of Grain Boundaries:
The force which is generated by grain island impingement is [145]
The volume of material included in a hemispherical island upon coalescence is
![]() . If the material in each island would spread uniformly over a
. If the material in each island would spread uniformly over a
![]() square area on the substrate, the uniform depth
square area on the substrate, the uniform depth ![]() would be
would be
![]() . The area of a lateral face of this equivalent material block is
. The area of a lateral face of this equivalent material block is
![]() , so that the uniform tensile stress on this surface which produces the same resultant force as in (9.2) is
, so that the uniform tensile stress on this surface which produces the same resultant force as in (9.2) is ![]() or
or ![]() . Therefore, the average intrinsic stress caused by coalescence in the film with thickness
. Therefore, the average intrinsic stress caused by coalescence in the film with thickness ![]() is [145]
is [145]
![]() Misfit Stress:
Misfit Stress:
Misfit stresses occur in crystalline films because of the lattice mismatch at the interface between film and substrate. If only the film lattice would adjust to the substrate lattice as demonstrated in Fig. 9.6b, the misfit strain in the film would be
![]() . But in reality the lattice of the film as well as the substrate are both adapted at the interface, which is characterized by the misfit parameter [146]
. But in reality the lattice of the film as well as the substrate are both adapted at the interface, which is characterized by the misfit parameter [146]
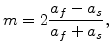 |
(9.4) |
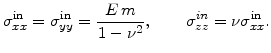 |
(9.5) |
![]() Grain Growth:
Grain Growth:
During grain growth some grain boundaries and their volumes disappear. Assume that ![]() is the pure crystal volume, where the excess volume of the grain boundaries is not included, and
is the pure crystal volume, where the excess volume of the grain boundaries is not included, and ![]() is the average grain diameter. Then the grain boundary area per unit volume is
is the average grain diameter. Then the grain boundary area per unit volume is ![]() for spherical grains. If
for spherical grains. If ![]() is the excess volume per unit area of the grain boundary, the total excess volume for the grain boundaries in a volume
is the excess volume per unit area of the grain boundary, the total excess volume for the grain boundaries in a volume ![]() is [133]
is [133]
![]() Excess Vacancy Annihilation:
Excess Vacancy Annihilation:
The gaps at the grain boundaries are closed by stretching the grains. The stress calculation is in principle the same as for the grain growth. If ![]() is the vacancy volume and
is the vacancy volume and ![]() is the atomic volume, then for a number of
is the atomic volume, then for a number of ![]() vacancies which annihilate per unit volume, the normalized volume change
vacancies which annihilate per unit volume, the normalized volume change
![]() . Therefore, the intrinsic stress caused by vacancy annihilation is given by [133]
. Therefore, the intrinsic stress caused by vacancy annihilation is given by [133]
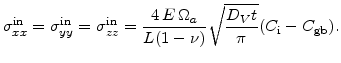 |
(9.12) |
![]() Thermal Stress:
Thermal Stress:
The developed intrinsic stress due to thermal mismatch in the film and in the substrate material is
| (9.13) |
![]() Insertion of Excess Atoms:
Insertion of Excess Atoms:
The insertion of excess atoms into the grain boundaries creates a compressive stress in the film [144]
In this work a methodology to predict a qualitative strain or stress curve over the film thickness was found. This methodology is based on the knowledge of the different intrinsic stress sources, the observed deflection characteristic of the deposited thin film material, and human mind. In the state of the art of development this methodology can not weight the influence of the different single stress sources in the different film thicknesses automatically. In order to find the strain or stress curve automatically a more advanced thin film stress model is necessary. The development of a thin film model, which takes all stress sources into account and weights them for different film materials and process conditions automatically, should be done in future work.