2.2.6 Electro-Thermal Coupling

As it was shown in the previous sections, the temperature is nearly always involved in parasitic effects and the temperature is mostly a result of electrical load. However, the temperature is a natural result of a system which dissipates power since it represents the change of the internal energy of the system as previously presented at the beginning of this chapter.

A common modeling approach for the heat source term in electro-magnetic systems can be expressed by (2.88) as

$\displaystyle {H_{\mathrm{th}}}{=}{\mathbf{{E}}} \cdot {\mathbf{{J}}} + {\mathb... ...tial}_{t}}{\mathbf{{D}}} + {\mathbf{{H}}} \cdot {{\partial}_{t}}{\mathbf{{B}}},$

(2.97)

where the first term shows the power loss density according to the applied electric field, where the second and the third terms present the internal power density of the electric and magnetic field, respectively.

This rigorous determination of the power density ${H_{\mathrm{th}}}$ couples the electro-magnetic and the thermal subsystems yields (2.9). For special materials which show for instance PELTIER^2.25 and SEEBECK effects, equation (2.97) has to be appropriately expanded by introducing an additional term accounting for these effects as proposed in [61,66] and reads

$\displaystyle - \mu^{\mathrm{th}} {\mathbf{{J}}} \cdot {{\boldmath {\nabla}}}{T},$

(2.98)

where the THOMSON coefficient $\mu^{\mathrm{th}}$ is defined by

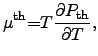$\displaystyle \mu^{\mathrm{th}} {=}T {\frac{\partial{P_{\mathrm{th}}}}{\partial{T}}},$

(2.99)

using the thermopower coefficient $P_{\mathrm{th}}$ , which is determined by the change of the contact voltage with respect to the temperature change [72]

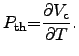$\displaystyle P_{\mathrm{th}}{=}{\frac{\partial{V_{\mathrm{c}}}}{\partial{T}}}.$

(2.100)

Stefan Holzer 2007-11-19