Next: 2.2.8 Mechanical Subsystem Up: 2.2 Heating Phenomena Previous: 2.2.6 Electro-Thermal Coupling Contents
A rather computational expensive but important effect for modern electronic devices is the volume expansion of condensed matter due to a temperature increase. From the microscopic point of view, the BROWNian motion increases with rising temperature. Therefore, the average distance of the particles at higher temperatures is larger than at lower temperatures. Hence, the volume of the unit cell has been expanded. For semiconductor devices that operate at nearly constant and moderate temperatures, a certain thermal volume expansion can be anticipated during the device design.
Because most design rules consider thermal equilibrium conditions between the operating device and its ambient, additional transient heat source terms which result for instance from self-heating can drastically enhance the volume expansions and result in wrong predictions of the device characteristics at certain operation conditions.
Generated heat in modern interconnect structures as well as in semiconductor devices can be taken into account by a certain average heat source distribution but this approach is still limited to experience of the past implementations and experiments. This is a major concern of modern reliability investigations, especially for novel interconnect structures and for high performance devices such as microprocessors and power amplifiers.
To account for the thermal volume expansion behavior, a first order approach
Some simulation tools might use higher order Ansatz functions, hence (2.47) can be adapted to
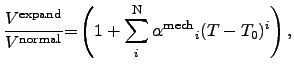 |
(2.102) |
To determine the elongation of a one-dimensional body, e.g. a rod, the
one-dimensional expansion coefficient can be derived from the volume
expansion coefficient
![]() from its definition
from its definition
| (2.106) |
The impact of a thermal expansion is manifold. If the volume is able to change its size, and there are no confinements to the volume, the consequence can be either shrinking or expansion. The more general case applies mostly: Confinements like adhesion and constrictions usually determine the volume expansion. Hence, the volume is bared by some other materials, which are not that compressible or elastic as required to allow an unconfined expansion. Therefore, strain and stress occur which are the mechanical driving forces for tension, contraction, torsion, and other effects including a change of the crystal structure, or phases.