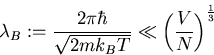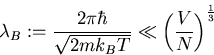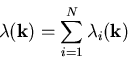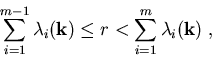

Next: 3.2 Selbststreuung
Up: 3 Monte-Carlo-Methode
Previous: 3 Monte-Carlo-Methode
In der semi-klassischen Beschreibung der Dynamik von Elektronen in einem Festkörper
geht man von punktförmigen
Teilchen aus, die sich auf wohldefinierten Bahnen bewegen. Das klassische Bild der Trajektorie setzt voraus, daß das Wellenpaket des untersuchten Teilchens lokalisiert sein muß, daß also dessen
Ausdehnung kleiner als der mittlere Teilchenabstand ist. Die
de-Broglie-Wellenlänge 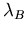 muß also folgende Ungleichung
muß also folgende Ungleichung
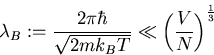 |
(3.1) |
erfüllen, da sonst nur eine ausschließlich quantenmechanische Betrachtung
möglich ist. Nach [JL89] kann man die Bedingung
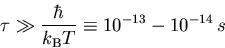 |
(3.2) |
aus der Heisenbergschen
Unschärferelation herleiten, die in der Praxis (bei endlichen Temperaturen) erfüllt ist.
Die Elektronenbahnen gehorchen dem Newtonschen Axiom
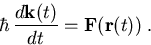 |
(3.3) |
Im Fall eines räumlich konstanten elektrischen Feldes 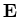 lautet die Lösung
lautet die Lösung
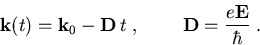 |
(3.4) |
Damit lautet die zeitliche Entwicklung der Bandformfunktion 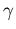 in einem nicht-parabolischen Band
in einem nicht-parabolischen Band
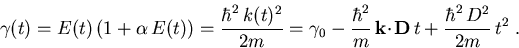 |
(3.5) |
Für die zeitliche Entwicklung der Gruppengeschwindigkeit ergibt sich damit
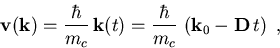 |
(3.6) |
wobei die energieabhängige effektive Leitfähigkeitsmasse mc als zeitlich konstant angenommen wurde. Damit wird der Ortsvektor der Teilchenbahn zu
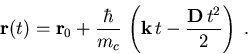 |
(3.7) |
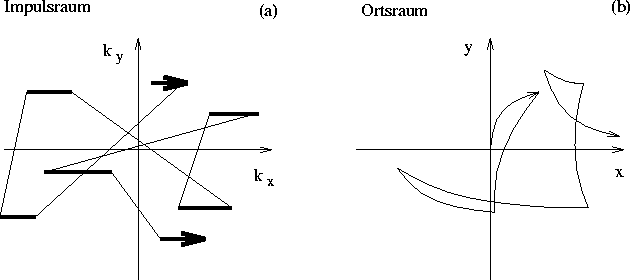
Die Bahnen sind im Ortsraum wie für freie Elektronen Parabeln, jedoch ist die
Masse eine Funktion der Energie (Abbildung 3.2).
Abbildung 3.2:
Die dicken Linien in (a) repräsentieren
den Anstieg des Impulses in Abhängigkeit der Zeit und entsprechen im Ortsraum (b)
einem parabelähnlichen freien Flug. Dünne Linien in
(a) stellen die Streuprozesse dar.
 |
(3.4) und (3.7) beschreiben vollständig das zeitliche Verhalten eines klassischen Teilchens
in einem Festkörper unter dem Einfluß eines konstanten Feldes bei Annahme eines nicht-parabolischen Bandes. Wäre der Festkörper streng periodisch, so gäbe es keinerlei
Wechselwirkung mit dem Elektron, und es könnte sich ungehindert im Festkörper bewegen. Aufgrund von räumlichen Asymmetrien infolge von Verunreinigungen oder thermischen Schwingungen kommt es zu Wechselwirkungen zwischen diesen
Störungszentren, die das Elektron von ihrer ursprünglichen Bahn
ablenken. Der Ausdruck 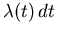 sei die Wahrscheinlichkeit, daß ein Teilchen zur
Zeit t gestreut wird. Unter der Annahme, daß ein Streuprozeß zur Zeit
sei die Wahrscheinlichkeit, daß ein Teilchen zur
Zeit t gestreut wird. Unter der Annahme, daß ein Streuprozeß zur Zeit 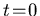 stattfindet lautet die Wahrscheinlichkeit P(t), daß das Teilchen
bis zur Zeit t keiner erneuten Streuung unterliegt, also eine freie Flugdauer t hat,
stattfindet lautet die Wahrscheinlichkeit P(t), daß das Teilchen
bis zur Zeit t keiner erneuten Streuung unterliegt, also eine freie Flugdauer t hat,
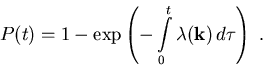 |
(3.8) |
Nach dieser Wahrscheinlichkeitsverteilung kann man eine statistische Folge von Driftzeiten erzeugen. Bei der direkten Methode [JR83] bestimmt man die Driftzeit 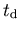 aus
aus
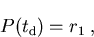 |
(3.9) |
wobei r1 eine gleichverteilte Zufallszahl zwischen 0 und 1 ist. Eingesetzt in (3.8) erhalten wir
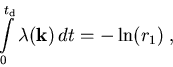 |
(3.10) |
wobei wir berücksichtigt haben, daß r1 gleichverteilt ist.
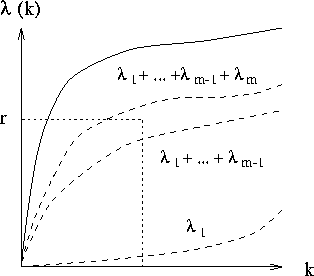
Abbildung 3.3:
Wahl des Streuprozesses mit Hilfe einer gleichverteilten Zufallszahl
r im Intervall [ ].
].
 |
Am Ende des freien Fluges wird mit Hilfe einer zweiten, im Bereich
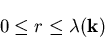 |
(3.11) |
gleichverteilten Zufallszahl r2 ein Streuprozeß ausgewählt. Die totale
Streurate 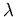 ist die Summe der einzelnen Streuraten N verschiedener
Streuprozesse:
ist die Summe der einzelnen Streuraten N verschiedener
Streuprozesse:
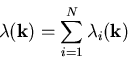 |
(3.12) |
Der m-te Streuprozeß wird ausgewählt, wenn gilt:
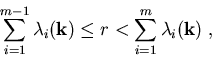 |
(3.13) |
wobei 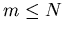 ist.
ist.


Next: 3.2 Selbststreuung
Up: 3 Monte-Carlo-Methode
Previous: 3 Monte-Carlo-Methode
Kaiblinger-Grujin Goran
1997-12-06