3.3 Mittelwertbildung

Der Zeitmittelwert einer physikalischen Observablen $A(\vec{k}(t))$, wie etwa der mittleren Teilchenenergie oder der mittleren Geschwindigkeit ist gegeben als [JL89]

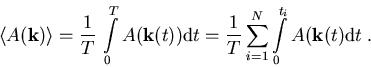$$\begin{eqnarray}\left<A(\vec{k})\right\gt = \frac{1}{T}\,\int\limits_0^T A(\vec{... ...sum\limits_{i=1}^N\int\limits_0^{t_i}A(\vec{k}(t){\mathrm d}t\; .\end{eqnarray}$$ (3.18)

Dabei wird die Trajektorie eines Teilchens bis zum Zeitpunkt T nachgebildet. In der Summendarstellung wird die Unterteilung der einzelnen freien Flugzeiten berücksichtigt. Da aber zu jedem freien Flug ein Integral ausgewertet werden muß, ist diese Art der Mittelwertbildung nicht empfehlenswert. Unter der Berücksichtigung, daß die stationäre Verteilungsfunktion proportional der Zahl der Ladungsträger $n(\vec{k})\Delta\vec{k}$ ist, die sich zur Zeit t in einer Umgebung $\Delta \vec{k}$um $\vec{k}$ befinden, kann die obige Formel einer Mittelwertberechnung als Summe des Produkts einer impulsabhängigen Verteilungsfunktion und der jeweiligen physikalischen Observablen [VSS⁺88,SRV88]

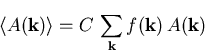$$\begin{eqnarray}\left<A(\vec{k})\right\gt = C\,\sum\limits_{\vec{k}}f(\vec{k})\,A(\vec{k})\end{eqnarray}$$ (3.19)

umgewandelt werden, wenn C eine Normierungskonstante darstellt. Bezieht man jetzt die Tatsache ein, daß die Elektronen ihre Zustände $\vec{k}$deterministisch ändern, so kann man die Elektronenverteilung mit

$$\begin{eqnarray}f(\vec{k}) = \frac{1}{\tau_0}f_b(\vec{k})\,\lambda^{-1}(\vec{k})\end{eqnarray}$$ (3.20)

beschreiben [JL89], worin $f_b(\vec{k})$ die Verteilungsfunktion des Teilchens unmittelbar vor der Streuung repräsentiert und proportional zu der Wahrscheinlichkeit ist, daß das Partikel in der Umgebung von $(\vec{k},\vec{r})$ anzutreffen sein wird. Dabei ist $\tau_0$ eine geeignete, noch zu untersuchende Normierungskonstante, die mit der Streuwahrscheinlichkeit in Verbindung gebracht werden kann [JL89]. Die Berechnung der Mittelwerte beschränkt sich also auf die Summation der physikalischen Größen vor dem Stoß. Einsetzen der obigen Gleichung in (3.19) ergibt nun für den Mittelwert $\left<A(\vec{k})\right\gt$ [SRV88]

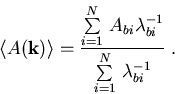$$\begin{eqnarray}\left<A(\vec{k})\right\gt = \frac{\sum\limits_{i=1}^N\,A_{bi}\lambda_{bi}^{-1}} {\sum\limits_{i=1}^N\, \lambda_{bi}^{-1}} \; .\end{eqnarray}$$ (3.21)

Im Fall, daß die gesamte Streurate konstant ist,

$$\begin{eqnarray}\lambda_{bi}=\Gamma, \quad\quad \forall\,\, i \leq N \; ,\end{eqnarray}$$ (3.22)

gehorcht der Mittelwert der folgenden Relation,

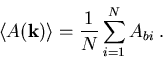$$\begin{eqnarray}\left<A(\vec{k})\right\gt = \frac{1}{N}\sum\limits_{i=1}^{N} A_{bi}\; .\end{eqnarray}$$ (3.23)