Next: B Schrödinger-Gleichung Up: Dissertation G. Kaiblinger-Grujin Previous: 6 Diskussion und Ausblick
![]()
![]()
![]()
Next: B
Schrödinger-Gleichung Up: Dissertation
G. Kaiblinger-Grujin Previous: 6
Diskussion und Ausblick
Der mittlere Abstand R benachbarter Störstellen läßt
sich schreiben als
| (A.1) |
mit einem Koeffizienten b, der von der Unterteilung des betrachteten
Volumens abhängt. Fragt man nach der Zahl der Störstellen in
einem Würfel der Kantenlänge R, so erhält man b=1
[Scl56]. Nimmt man eine Kugel mit Durchmesser
R so folgt b = 0.62. Ridley [KF89]
erhält auf Grund wahrscheinlichkeitstheoretischer Überlegungen
für ![]() .
.
Um die Willkürlichkeit bezüglich der geometrischen Unterteilung
zu umgehen, kann man sich folgendes überlegen. Der effektive Bohr-Radius,
der ein Maß für die räumliche Ausdehnung des gebundenen
Elektrons der Störstelle in einem Halbleiter darstellt, ist gegeben
durch
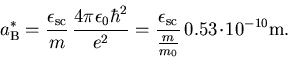 |
(A.2) |
Mit ![]() und
und ![]() erhalten wir für den Bohr-Radius in Si etwa 17 Å, während
der Abstand zweier Si-Atome im Gitter 2.35
erhalten wir für den Bohr-Radius in Si etwa 17 Å, während
der Abstand zweier Si-Atome im Gitter 2.35 ![]() ist. Bei niedriger Dotierung überlappen die H-ähnlichen Wellenfunktionen
der Donatorelektronen nicht, sodaß bei T=0 der Halbleiter
ein Isolator ist. Mit zunehmender Dotierung überlappen die Wellenfunktionen,
sodaß der Übergang vom Isolator zum Metall erfolgt (Mott-Übergang).
Dieser fließende Übergang von lokalisierten zu freien Elektronen
entsteht, wenn der durchschnittliche Abstand der Störstellen vergleichbar
wird mit dem effektiven Bohr-Radius aB*. Dann
geht die Ionisierungsenergie der Störstelle gegen Null, sodaß
das Elektron sich frei bewegen kann. Wir erhalten die Gleichung
ist. Bei niedriger Dotierung überlappen die H-ähnlichen Wellenfunktionen
der Donatorelektronen nicht, sodaß bei T=0 der Halbleiter
ein Isolator ist. Mit zunehmender Dotierung überlappen die Wellenfunktionen,
sodaß der Übergang vom Isolator zum Metall erfolgt (Mott-Übergang).
Dieser fließende Übergang von lokalisierten zu freien Elektronen
entsteht, wenn der durchschnittliche Abstand der Störstellen vergleichbar
wird mit dem effektiven Bohr-Radius aB*. Dann
geht die Ionisierungsenergie der Störstelle gegen Null, sodaß
das Elektron sich frei bewegen kann. Wir erhalten die Gleichung
| (A.3) |
Nach b aufgelöst ergibt sich
| (A.4) |
Für Si wird eine kritische Dotierung von ![]() cm-3 gemessen [Kit86]. Damit
erhalten wir
cm-3 gemessen [Kit86]. Damit
erhalten wir ![]() .
Andererseits lautet das Mott-Kriterium
.
Andererseits lautet das Mott-Kriterium
| (A.5) |
welches experimentell für Systeme bestätigt wurde, in denen
Nc über 9 Größenordnungen variiert![]() .
Das würde bedeuten, daß der durchschnittliche Abstand der Störstellen
zirka vier Bohr-Radien entspricht und
.
Das würde bedeuten, daß der durchschnittliche Abstand der Störstellen
zirka vier Bohr-Radien entspricht und ![]() ist.
ist.
Andererseits unterscheiden sich die Ionisationsenergien für unterschiedliche Donatoren in Silizium. Das wiederum bedeutet, daß auch der effektive Bohr-Radius unterschiedlich sein muß, was experimentell nachgewiesen wurde. Es konnte festgestellt werden, daß das Mott-Kriterium für unterschiedliche Dopanden in Si verschiedene Werte ergibt [CL75]. Strenggenommen bedeuten das, daß damit auch der mittlere Abstand benachbarter Störstellen vom Dopandentyp abhängt.
Da Sb in Si die geringste Ionisationsenergie besitzt, muß das
Donatorelektron besonders weit vom Kern sein, was wiederum den relativ
großen effektven Bohr-Radius impliziert. Lose gebunde Elektronen
sind besonders stark polarisierbar, was einen besonders starken Anstieg
von ![]() mit sich bringt, wenn sich die Dotierung der kritischen Dotierung Nc
nähert [CL75].
mit sich bringt, wenn sich die Dotierung der kritischen Dotierung Nc
nähert [CL75].