

Next: 1.2 Streuphasenanalyse
Up: 1 Theoretische Grundlagen der Streuung
Previous: 1 Theoretische Grundlagen der Streuung
Wir wollen von einem Potential ausgehen, das für 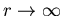 schneller als 1/r gegen Null geht. Nach (B.4) läßt sich die Schrödinger-Gleichung
für ein Teilchen der Masse m und dem Impuls
schneller als 1/r gegen Null geht. Nach (B.4) läßt sich die Schrödinger-Gleichung
für ein Teilchen der Masse m und dem Impuls 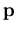 unter dem Einfluß eines solchen Potentials V(r) schreiben als
unter dem Einfluß eines solchen Potentials V(r) schreiben als
![\begin{displaymath}
\left[ \bigtriangleup +k^2 - U(r) \right] \Psi(\vec{r})=0\;,\qquad\quad U(r)\equiv\frac{2\,m V(r)}{\hbar^2} \; .
\end{displaymath}](img82.gif) |
(1.1) |
Wir suchen eine Lösung von (1.1), die asymptotisch der Summe einer ebenen Welle und einer auslaufenden Kugelwelle entspricht,
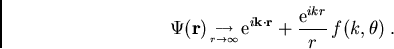 |
(1.2) |
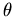 ist der Winkel zwischen dem Wellenvektor
ist der Winkel zwischen dem Wellenvektor 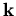 des Elektrons vor der Streuung und dem Wellenvektor
des Elektrons vor der Streuung und dem Wellenvektor 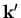 des Elektrons nach der Streuung.
des Elektrons nach der Streuung. 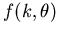 ist die Streuamplitude.
Zur Beschreibung von Streuexperimenten definiert man nun Wirkungsquerschnitte, die in direktem Zusammenhang mit dem asymptotischen Verhalten der stationären Lösung (1.2) stehen.
ist die Streuamplitude.
Zur Beschreibung von Streuexperimenten definiert man nun Wirkungsquerschnitte, die in direktem Zusammenhang mit dem asymptotischen Verhalten der stationären Lösung (1.2) stehen.
Der differentielle Streuwirkungsquerschnitt 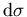 ist definiert als die Intensität der gestreuten Welle im Raumwinkel
ist definiert als die Intensität der gestreuten Welle im Raumwinkel 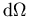 [WO75]:
[WO75]:
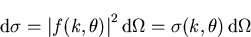 |
(1.3) |
Der totale Streuwirkungsquerschnitt 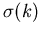 ist dann das Integral von (1.3) über den Raumwinkel:
ist dann das Integral von (1.3) über den Raumwinkel:
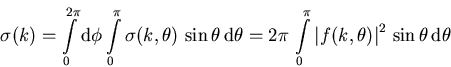 |
(1.4) |
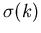 hat die Dimension einer Fläche und ist ein Maß für die totale Wahrscheinlichkeit, daß ein
Teilchen der Energie E(k) in einem Potential V(r) gestreut wird.
Das Streuproblem ist also gelöst, wenn man
hat die Dimension einer Fläche und ist ein Maß für die totale Wahrscheinlichkeit, daß ein
Teilchen der Energie E(k) in einem Potential V(r) gestreut wird.
Das Streuproblem ist also gelöst, wenn man 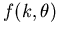 für ein bestimmtes Potential
V(r) kennt. Es gibt prinzipiell zwei Lösungsansätze. Man kann einerseits die Streuphasenanalyse benutzen, die Streuamplitude und ebene Welle in Legendre-Polynome und sphärische Bessel-Funktionen entwickelt. Da diese numerische Methode den exakten
Wirkungsquerschnitt liefert, wurde sie schon früh zur Beschreibung der niederenergetischen Streuung von Elektronen an ionisierten Störstellen benutzt
[Bla57,MB81].
Andererseits läßt sich die Schrödinger-Gleichung in eine Integralgleichung transformieren, deren Kern die Green-Funktion ist und als Fredholm-Integralgleichung bekannt ist [MF53a,MF53b,Moi70,MO70].
Diese Integralgleichung kann auf mehrere Arten gelöst werde.
Die wohl berühmteste und einfachste Methode ist die Born-Näherung für ebene Wellen (BA), bei der die Lösungsfunktion in eine Potenzreihe nach der Störung entwickelt wird. Ein Vergleich verschiedener Approximationen mit Hilfe ebener Wellen findet sich in [ED72]. Um die bekannten
Konvergenzprobleme von Potenzreihen zu umgehen, wurde andere Reihenentwicklungen mit
größerem Konvergenzradius vorgeschlagen [JP51,Mic69,Moi70,MO70,HS74,Kop84].
In den letzten Jahrzehnten wurden auch Variationsmethoden erfolgreich zur
Lösung von Streuproblemen herangezogen [Kat51,Moi66,Moi74,KFH76,Kop84].
für ein bestimmtes Potential
V(r) kennt. Es gibt prinzipiell zwei Lösungsansätze. Man kann einerseits die Streuphasenanalyse benutzen, die Streuamplitude und ebene Welle in Legendre-Polynome und sphärische Bessel-Funktionen entwickelt. Da diese numerische Methode den exakten
Wirkungsquerschnitt liefert, wurde sie schon früh zur Beschreibung der niederenergetischen Streuung von Elektronen an ionisierten Störstellen benutzt
[Bla57,MB81].
Andererseits läßt sich die Schrödinger-Gleichung in eine Integralgleichung transformieren, deren Kern die Green-Funktion ist und als Fredholm-Integralgleichung bekannt ist [MF53a,MF53b,Moi70,MO70].
Diese Integralgleichung kann auf mehrere Arten gelöst werde.
Die wohl berühmteste und einfachste Methode ist die Born-Näherung für ebene Wellen (BA), bei der die Lösungsfunktion in eine Potenzreihe nach der Störung entwickelt wird. Ein Vergleich verschiedener Approximationen mit Hilfe ebener Wellen findet sich in [ED72]. Um die bekannten
Konvergenzprobleme von Potenzreihen zu umgehen, wurde andere Reihenentwicklungen mit
größerem Konvergenzradius vorgeschlagen [JP51,Mic69,Moi70,MO70,HS74,Kop84].
In den letzten Jahrzehnten wurden auch Variationsmethoden erfolgreich zur
Lösung von Streuproblemen herangezogen [Kat51,Moi66,Moi74,KFH76,Kop84].


Next: 1.2 Streuphasenanalyse
Up: 1 Theoretische Grundlagen der Streuung
Previous: 1 Theoretische Grundlagen der Streuung
Kaiblinger-Grujin Goran
1997-12-06
![]() ist definiert als die Intensität der gestreuten Welle im Raumwinkel
ist definiert als die Intensität der gestreuten Welle im Raumwinkel ![]() [WO75]:
[WO75]: