Next: D Thomas-Fermi-Abschirmlänge Up: Dissertation G. Kaiblinger-Grujin Previous: B.2 Schrödinger-Gleichung des idealen Kristalls
![]()
![]()
![]()
Next: D
Thomas-Fermi-Abschirmlänge Up: Dissertation G. Kaiblinger-Grujin Previous: B.2
Schrödinger-Gleichung des idealen Kristalls
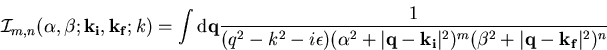 |
(C.1) |
mit ![]() nennt man Dalitz-Integrale [Dal51].
nennt man Dalitz-Integrale [Dal51].
Durch die Substitutionen
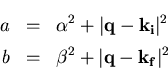 |
(C.2) |
und unter Benutzung der Feynman-Identität [Joa75]
![\begin{displaymath}\frac{1}{a^{m}b^{n}}= \frac{(m+n-1)!}{(m-1)!(n-1)!} \int\limi... ...\frac{t^{m-1}(1-t)^{n-1}}{[at + b (1-t)]^{m+n}} \,{\mathrm d}t\end{displaymath}](img718.gif) |
(C.3) |
läßt sich (C.1) schreiben
als
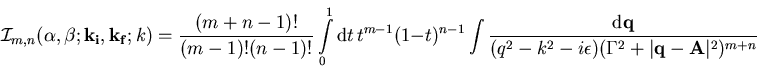 |
(C.4) |
mit
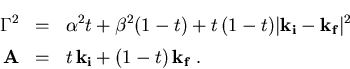 |
(C.5) |
Wir erhalten ein eindimensionales Integral in t und ein Raumintegral
der Form
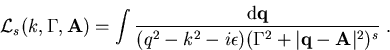 |
(C.6) |
Setzt man s=1 und legt die z-Achse des Vektors ![]() in Richtung von
in Richtung von ![]() ,
so erhält man
,
so erhält man
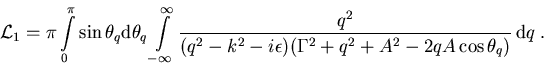 |
(C.7) |
Nach kurzer Nebenrechnung erhält man unter Zuhilfenahme des Residuensatzes
| (C.8) |
Durch sukzessives Differenzieren nach ![]() ergibt sich [Joa75]
ergibt sich [Joa75]
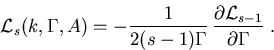 |
(C.9) |
Betrachten wir den Fall m=n=1 mit ![]() , so erhält man für (C.1) unter
Verwendung von (C.5)
, so erhält man für (C.1) unter
Verwendung von (C.5)
![\begin{eqnarray}{\cal I}_{1,1} & = & \int\limits_{0}^{1} {\cal L}_{2} (k,\Gamm... ...}t}{ \Gamma [ 2ik\Gamma - ( \alpha^2 t + \beta^2 (1-t) ) ] } \; .\end{eqnarray}](img729.gif) |
(C.10) |
Durch die rationale Transformation
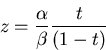 |
(C.11) |
geht (C.10) über in
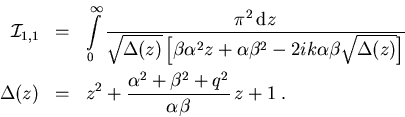 |
(C.12) |
Unter Verwendung des Satzes von Vieta kann man nun ![]() durch seine Wurzeln z1 und z2 darstellen,
durch seine Wurzeln z1 und z2 darstellen,
| (C.13) |
Durch Übergang auf die Variable
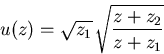 |
(C.14) |
läßt sich (C.12) überführen
in
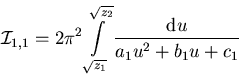 |
(C.15) |
mit
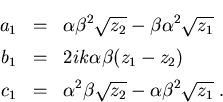 |
(C.16) |
Da die Koeffizienten des Integranden in (C.15)
nicht positiv definit sind, müssen wir noch folgende Transformation
durchführen:
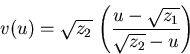 |
(C.17) |
(C.15) wird damit zu
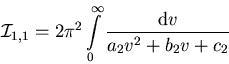 |
(C.18) |
mit
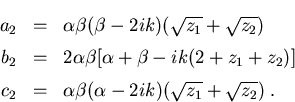 |
(C.19) |
Das Integral (C.18) ist elementar und
hat die Lösung
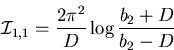 |
(C.20) |
mit D2= b22-4a2c2.