6.4.3.2 Multiple Shooting

Reduced superposition has the big advantage that the number of integrations is halved, i.e., instead of N only N/2 have to be performed to obtain the final IVP. The stability is also increased due to the smaller dimension of the matrices. This second advantage, however, does not suffice to guarantee convergence in all cases. Multiple shooting is a strategy that significantly enhances the stability of the shooting method. The simple but very powerful idea behind is to integrate the ODE not over the full interval in one step but split the interval into N_p sub-intervals as shown in Figure 6.4. At the ending points z_p--the so-called shooting points--the solution is reorthogonalized. Thereby damped and growing modes are decoupled. This general and heuristic statement can be put on a mathematical sound basis. A detailed justification and discussion of the operation principle and the benefits can be found in [200, pp. 145-165] where the proposed stability is also theoretically proven.^f

We will only outline the principle of multiple shooting employing reorthogonalization and decoupling. Additionally, compactification is applied--a technique that leads to formulae that can be evaluated recursively. The storage demands of the algorithm are thus not increased in comparison to the previous ones and the performance with respect to stability is not degraded due to the separated BCs.^g Both properties are of utmost importance for our application. The description of this so-called stabilized march algorithm is divided into three different parts since the first and last sub-interval have to be treated individually. 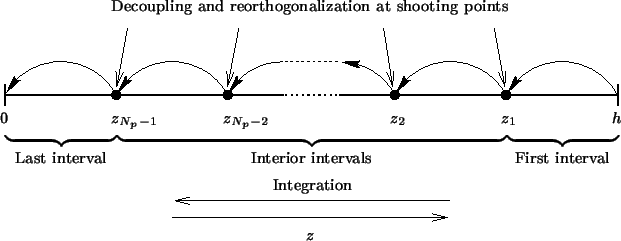A graphical illustration of the algorithm, especially the integration direction and the multiple shooting technique, is shown in Figure 6.4.

  

Figure 6.4: Multiple shooting employing decoupling and reorthogonalization at the shooting points z_p forms the basis of the stabilized march algorithm. In our implementation we integrate the IVP in opposite direction to the z-axis, i.e., from z = h to z = 0.

First interval (p = 1). In the first interval z $\in$ [z₁, h] we carry out Step 1 and Step 2 of the shooting algorithm using reduced superposition (cf. Table 6.3), i.e., we perform a QR-factorization of the boundary matrix $\underline{\mathbf{B}}_{h}^{\mathrm{H}}$ to determine the initial values $\underline{\mathbf{\widehat{V}}}_{1}^{}$(h) = $\underline{\raisebox{0pt}[1ex][0pt]{$\mathbf{Q}$}}_{h}^{2}$ at the first starting point z₀ = h, and integrated then the IVP

$$\underline{\mathbf{\widehat{V}}}_1^\prime(z) = \underline{\mathbf... ...bf{\widehat{V}}}_1(h) = \underline{\raisebox{0pt}[1ex][0pt]{$\mathbf{Q}$ }}_h^2$$ (6.46)

to obtain N/2 linearly independent solutions $\underline{\mathbf{\widehat{V}}}_{1}^{}$(z₁) at the opposite ending point z₁ of the interval.

Interior intervals (p = 2,..., N_p - 1). For the interior intervals z $\in$ [z_p, z_{p - 1}] we first determine the initial values $\underline{\mathbf{\widehat{V}}}_{p}^{}$(z_{p - 1}) at the starting point z_{p - 1}. Simply using the integrated solution $\underline{\mathbf{\widehat{V}}}_{p-1}^{}$(z_{p - 1}) from the previous interval would be identical to single shooting. A common choice is taking any orthogonal matrix independently from the previous interval. The algorithm is then referred to standard multiple shooting [200, pp. 146-148] and has the big advantage that the integrations within the N_p sub-intervals can be performed parallel. However, all coefficient matrices $\underline{\mathbf{\widehat{S}}}_{p}^{}$ have to be stored individually. After integration they are determined by matching the solutions at the shooting points z_p. To obtain a stable algorithm this has to be done simultaneously [200, pp. 149-153], i.e., a linear algebraic equation system with N_p x N/2 unknowns and N_s right-hand sides has to be solved. Although this equation system is band-limited with bandwidth N/2 the storage demands are dramatically increased by the number N_p of sub-intervals. A dangerously appealing idea is to evaluate the relations recursively. The memory consumption would be the same as for single shooting with reduced superposition but the stability properties are almost lost. This method, usually called multiple shooting with compactification [200, pp. 153-155], is therefore not suited for our application.

However, if the initial values are not independently chosen from the previous interval the algorithm thus obtained becomes stable and is said to employ marching techniques [200, pp. 155-164]. In order to achieve stability, it is necessary to monitor the growth of the fundamental modes. Otherwise the growing modes would quickly get dominant and the linear independence would get lost numerically due to the finite numeric precision of computers. Such a monitoring is realized by reorthogonalization or decoupling that is done by QR-factorization of the integrated solution matrix $\underline{\mathbf{\widehat{V}}}_{p-1}^{}$(z_{p - 1}) of the previous interval p - 1, i.e.,

$$\underline{\mathbf{\widehat{V}}}_{p-1}(z_{p-1}) = \underline{\raisebox{0pt}[1ex][0pt]{$\mathbf{Q}$ }}_{p-1}\underline{\mathbf{R}}_{p-1}.$$ (6.47)

Choosing the orthogonal part, i.e., the matrix $\underline{\raisebox{0pt}[1ex][0pt]{$\mathbf{Q}$}}_{p-1}^{}$ as the initial values, i.e.,

$$\underline{\mathbf{\widehat{V}}}_p(z_{p-1}) = \underline{\raisebox{0pt}[1ex][0pt]{$\mathbf{Q}$ }}_{p-1},$$ (6.48)

it can be shown that the growing and damped modes are effectively decoupled [200, pp. 157-159] and good convergence is thus guaranteed. Note that the complete separation of the BCs at z = 0 and z = h is crucial for the success of the stabilized march technique.

Last interval p = N_p. For the last interval z $\in$ [0, z_{Np - 1}] the QR-factorization of the integrated solution $\underline{\mathbf{\widehat{V}}}_{N_p}^{}$(0) is skipped. The coefficient matrix $\underline{\mathbf{\widehat{S}}}_{N_p}^{}$ is calculated by enforcing the BCs valid at z = 0, i.e.,

$$\underline{\mathbf{B}}_0\underline{\mathbf{\widehat{V}}}_{N_p}(0)\underline{\mathbf{\widehat{S}}}_{N_p} = \underline{\mathbf{A}}.$$ (6.49)

Once this linear equation system is solved for $\underline{\mathbf{\widehat{S}}}_{N_p}^{}$ with LU-factorization, the initial values $\underline{\mathbf{U}}$(0) at z = 0 are obtained from

$$\underline{\mathbf{U}}(0)=\underline{\mathbf{\widehat{V}}}_{N_p}(0)\underline{\mathbf{\widehat{S}}}_{N_p}.$$ (6.50)

The resulting IVP is finally integrated to determine the solution $\underline{\mathbf{U}}$(z) of the BVP (6.52) at any desired vertical position. These steps are summarized in Table 6.4 that describes the stabilized march algorithm. The numerical costs are discussed in the following section.

  

Table 6.4: Algorithm for stabilized march technique.

Footnotes

... proven.^f

The proof is given in great length in Section 4.4.2 of [200, pp. 157-159].

... BCs.^g

Stability of decoupling in combination with compactification is proved in Lemma 4.53 on page 157 and Theorem 4.58 on page 159 of [200].