



Next: 6.4.3.2 Multiple Shooting
Up: 6.4.3 Shooting Method
Previous: Single Shooting
In case of single shooting the ODE system
has to be integrated N + Ns times: N times to determine the fundamental
solution matrix
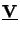 (h) at the opposite boundary point z = h and another
Ns times to determine the BVP solutions
(h) at the opposite boundary point z = h and another
Ns times to determine the BVP solutions
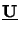 (z) subject to the
Ns BCs since the fundamental solution matrix is not stored
at each mesh point to keep the memory demands small.
However, the N BCs are equally separated at
the two ending points z = 0 and z = h. It suffices to integrate
the ODE system only N/2 times to relate both boundaries
as will be shown. Since N/2 BCs are given at one
point we can express the solution
u(z) of our
separated BVP by a reduced superposition like
(z) subject to the
Ns BCs since the fundamental solution matrix is not stored
at each mesh point to keep the memory demands small.
However, the N BCs are equally separated at
the two ending points z = 0 and z = h. It suffices to integrate
the ODE system only N/2 times to relate both boundaries
as will be shown. Since N/2 BCs are given at one
point we can express the solution
u(z) of our
separated BVP by a reduced superposition like
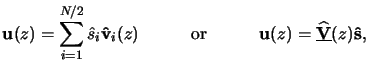 |
(6.41) |
whereby
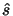 is a N/2-dimensional coefficient vector and the
N x N/2-dimensional matrix
is a N/2-dimensional coefficient vector and the
N x N/2-dimensional matrix
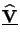 (z) carries the N/2
linearly independent
(z) carries the N/2
linearly independent
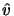 i(z) spanning the vector space
i(z) spanning the vector space
 N x N/2. Now the initial values cannot be
chosen arbitrarily. On the contrary, they have to fulfill the N/2 BCs
at one ending point. Since we have homogeneous BCs at the lower
interface at z = h we determine
N x N/2. Now the initial values cannot be
chosen arbitrarily. On the contrary, they have to fulfill the N/2 BCs
at one ending point. Since we have homogeneous BCs at the lower
interface at z = h we determine
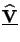 (h) at this point, i.e.,
we search for a matrix
(h) at this point, i.e.,
we search for a matrix
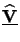 (h) that obeys
(cf. (6.51))
(h) that obeys
(cf. (6.51))
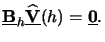 |
(6.42) |
For that we calculate the QR-factorization [202, pp. 223-236] of the
complex-conjugate transposed or Hermitian of the boundary matrix
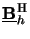
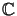 N x N/2
(cf. Table 6.1),
N x N/2
(cf. Table 6.1),
 |
(6.43) |
Here,
![$ \underline{\raisebox{0pt}[1ex][0pt]{$\mathbf{Q}$}}_{h}^{}$](img969.gif)
 N x N is an orthogonal matrix,
whereas
N x N is an orthogonal matrix,
whereas
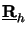
 N x N/2 is upper triangular.
The two sub-matrices
N x N/2 is upper triangular.
The two sub-matrices
![$ \underline{\raisebox{0pt}[1ex][0pt]{$\mathbf{Q}$}}_{h}^{1,2}$](img975.gif) are of dimension
N x N/2,
and
are of dimension
N x N/2,
and
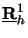 and
and
 are
N/2 x N/2-dimensional.
Since the inverse of an orthogonal matrix simply equals its Hermitian
we obtain
are
N/2 x N/2-dimensional.
Since the inverse of an orthogonal matrix simply equals its Hermitian
we obtain
![$\displaystyle \underline{\raisebox{0pt}[1ex][0pt]{$\mathbf{Q}$ }}_h^{{\mathrm{H...
...x][0pt]{$\mathbf{Q}$ }}_h^2 &= \underline{\mathbf{0}}.\end{cases}\hspace*{-2cm}$](img978.gif) |
(6.44) |
The last equation is the required BC (6.63), and we thus have
![$\displaystyle \underline{\mathbf{\widehat{V}}}(h) = \underline{\raisebox{0pt}[1ex][0pt]{$\mathbf{Q}$ }}_h^2.$](img979.gif) |
(6.45) |
The missing steps equal those performed in simple shooting
(cf. Table 6.2). The big advantage stems from the fact
that we halved the number of required integrations to obtain the linearly
independent solution matrix at the opposite interval boundary
(cp. (6.56) with (6.62)).
The reduced superposition algorithm is
summarized in Table 6.3. Numerical problems are moderated
since the size of the linear equations system is also halved--compare
Step 3 of Table 6.3 with Step 2
of Table 6.2--and can thus be inverted in a more stable way.
As a final remark note that the ODE is now integrated in ``opposite'' direction
as before, i.e., from z = h to z = 0 (cf. Figure 6.4).
Table 6.3:
Algorithm for
shooting with reduced superposition.
 |




Next: 6.4.3.2 Multiple Shooting
Up: 6.4.3 Shooting Method
Previous: Single Shooting
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
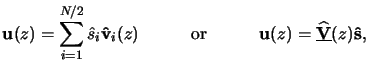
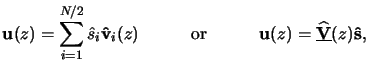
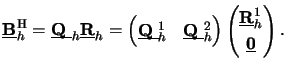
![$\displaystyle \underline{\raisebox{0pt}[1ex][0pt]{$\mathbf{Q}$ }}_h^{{\mathrm{H...
...x][0pt]{$\mathbf{Q}$ }}_h^2 &= \underline{\mathbf{0}}.\end{cases}\hspace*{-2cm}$](img978.gif)