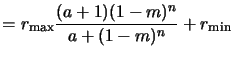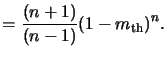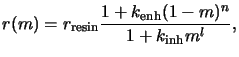7.2.1 Development Rate Modeling

There exists a wide range of rate models ranging from purely empirical fits to physical based approaches. We first describe the three most prominent analytical models and then present well-established experimental results that were obtained for the already mentioned IBM APEX-E resist (cf. Table 7.1). Dill's `E'-model. Along with the `ABC'-model describing the exposure/bleaching phenomenon Frederick Dill also introduced a rate model [74]. The dependence of the local development rate r(m) on the normalized local PAC concentration m is thereby given by the three-parameter equation

 

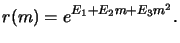$$r(m) = e^{E_1 + E_2m + E_3m^2}.$$ (7.18)

The three parameters E₁, E₂, and E₃ are obtained using least-square fitting to experimental data. Experience shows that the relationship (7.20) is capable of attaining good agreement with data at high values of the inhibitor concentration m. However, it does not properly characterize rates at low concentrations since it predicts an unphysical rate maximum in this regime. This can usually be ignored since the development rate for small m is so high that it can be considered infinite anyway [74,208]. Dill's `E'-model was the default model of early versions of the lithography simulator SAMPLE [109]. Nowadays, it is often used because of its obvious simplicity.

Kim's `R'-model. Deok Kim et al. addressed in [75] the shortcomings of Dill's `E'-model. Two assumption were made to obtain a more realistic expression to fit experimental rate data: Firstly, the chemical reaction at the resist/developer interface is postulated to be the rate-limiting process, which implies that the mass-transfer dynamics, i.e., the diffusion process, can be neglected. Secondly, the time required to dissolve a differential resist layer is assumed to consist of two additive terms: (i) the time required to dissolve all the PAC in the layer, and (ii) the time required to dissolve the photo-produced acid and all other compounds. With these assumptions the resulting rate expression can be written as

 

$$r(m)=\left[\dfrac{1-me^{-R_3(1-m)}}{R_1}+\dfrac{me^{-R_3(1-m)}}{R_2}\right]^{-1},$$ (7.19)

whereby R₁ is the dissolution rate of a fully exposed resist (m = 0), R₂ of an unexposed resist (m = 1), and R₃ is a sensitivity parameter with the interpretation of a rate enhancement due to photoinduced acid. The first two parameters R₁ and R₂ can be measured, whereas the third R₃ has to be fitted. The proposed relation (7.21) contains only three parameters. However, several additional R-parameters can be included in an extended version to account for surface induction effects. The depth dependent rate is then modeled by

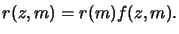$$r(z,m)=r(m)f(z,m).$$ (7.20)

The induction multiplier f (z, m) depends on the depth z into the resist as well as on the PAC m. By choosing a decaying exponential function for the vertical dependence like

$$f(z,m) = 1 - (1-f(0,m))e^{-z/R_4}\vspace*{-5mm}$$ (7.21)
with

$$f(0,m) = (1-m)R_5 + mR_6$$ (7.22)

an excellent agreement with measured data over the full exposure range is obtained [75,209]. The parameters R₅ and R₆ describe the ratio between surface and bulk rates for full and no exposure, respectively. R₄ is the characteristic retardation depth and is in principle only determined by the resist and its processing. For certain resists the ratio of the surface and bulk rate f (0, m) is a discontinuous function in the PAC m. This can simply be accounted for by piecewise linear equations similar to that proposed in (7.24) [75]. Kim's `R'-model is the second rate model available in the lithography simulator SAMPLE [209].

Mack's `a'-model. Both so far described models provide mainly fitting formulae with parameters having minor or no physical meaning. Chris Mack proposed a four parameter model based on simple kinetic considerations with the advantage that all involved parameters have physical significance [107,210]. The approach relies on the assumption that the development process involves two dominating mechanisms, namely the diffusion of the developer from the bulk solution to the resist surface and the reaction of the developer with the resist. Modeling the rates of both reactions with fundamental kinetic theory and equating them yields

$$r(m) = r_{\mathrm{max}}\frac{(a+1)(1-m)^n}{a+(1-m)^n} + r_{\mathrm{min}}\vspace*{-5mm}$$ (7.23)
with

$$a = \frac{(n+1)}{(n-1)}(1-m_{\mathrm{th}})^n.$$ (7.24)

Here r_min is the development rate of the unexposed resist, whereas r_max is the rate of the fully exposed resist. The latter statement is true provided that the experimental observation r_min $\ll$ r_max holds. n is a selectivity parameter that describes the kinetic order of the dissolution reaction occurring at the resist surface. The parameter m_th is a threshold PAC concentration corresponding to the concentration at which the development curve displays an inflection point. It can thus be interpreted as the concentration of a transition between fast and slow development regimes.

The kinetic model (7.25) is based on the principle of dissolution enhancement, i.e., it is assumed that the acid enhances the dissolution of the resin/PAC mixture. In reality this is a simplification--there is a second mechanism at work. The PAC acts to inhibit dissolution of the resin while the acid acts to enhance the dissolution. An enhanced kinetic model including both effects was proposed in [90] and takes the form

 

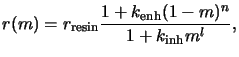$$r(m) = r_{\mathrm{resin}}\frac{1+k_{\mathrm{enh}}(1-m)^n} {1+k_{\mathrm{inh}}m^l},$$ (7.25)

where k_enh is the rate constant for the enhancement mechanism of order n, and k_inh is the rate constant for the inhibition mechanism of order l. r_resin stands for the development of the resin alone. The enhanced Mack model is a superset of the original `a'-model that neglects the inhibition phenomenon. Setting k_inh = 0 both Mack models (7.25) and (7.27) are equal for the case that a is very large. A large a implies a slow surface reaction in comparison to the mass transport of the developer, i.e., the inflection point m_th is negative (cf. (7.26)) meaning that the development process is only governed by one process. This requirement for the comparison stems from the fact that the enhanced Mack model does not account for the diffusion of the developer.

Finally, an empirical model like (7.24) can be used to describe the positional dependence of the development rate. Both Mack models are implemented in the PROLITH lithography simulator [108].

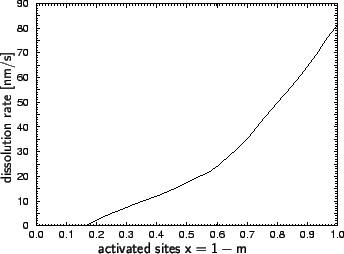
Experimental data for chemically amplified resists. The dissolution rate of a positive deblocking chemically amplified resist system is assumed to be a property of the deprotection level of the polymer. This relationship can be determined from the measurements of Nick Eib et al. for the IBM APEX-E resist [93]. The measured data show the dissolution rate versus exposure. Performing an exposure simulation and applying the post-exposure bake model of (7.16) the relation between rate and deprotection level can be extracted. The thus obtained results are plotted in Figure 7.2. A similar procedure is typically used for the development simulation of other chemically amplified resists since the physical processes are still not fully understood so that no physically meaningful model has been provided until yet.

  

Figure 7.2: Development rate of the IBM APEX-E chemically amplified resist as a function of the normalized deprotection level x = 1 - m (after [93]).