String algorithm. One of the first attempts to model the surface advancement goes back to Robert Jewett et al., who proposed the so-called string algorithm in [211,212]. We shall explain the operation principle in two spatial dimensions only. The extension to the third dimension is obvious. The surface is approximated by a series of points joined by straight line segments forming a string. Each point advances along the angle bisector of the two adjoining segments according to the local value of the development or etch rate. During the simulation, the segments are kept roughly equal in length by adding points in regions of expansion of the front, and by deleting points in regions of contraction. Problems are due to loop formation, which especially occurs in case of highly varying spatial rate distributions [213]. Initially small loops develop in the surface, but as the simulation continues, these loops begin to expand and also intersect with each other. The destructive loop behavior is actually caused by the string algorithm itself. During the movement of the segments the normal vectors have to be determined from the local surface. The finite numerical precision results in an inaccurate calculation of the subsequent normal vectors. These errors accumulate and the algorithm fails. To avoid this problem, it is necessary to remove the loops before they become too complex. This ``delooping'' operation has to be performed every few time-steps [213]. For that purpose the intersection of all the segments in the string must be found so that the loops can be deleted. In two dimension these problems can be solved with moderate computational expense. Although the extension to the third spatial dimension is conceptually obvious, it is far away from just replacing the line segments with a triangular surface mesh. The required operations for a stable performance are quite computation expensive. Instead of cutting lines the intersections of faces have to be calculated, which introduces additional error sources. Strong efforts were made to develop efficient loop detection and removal algorithms [109,214,215,209]. The string algorithm is now claimed to be stable also in three spatial dimensions [110,216,213,217,218]. It is the surface advancement algorithm of the SAMPLE lithography simulator in two as well as three dimensions [219].
Level set methods. Level set methods have recently been introduced
by Stanley Osher and James Sethian [220]. They are based on solving a
Hamilton-Jacobi type equation for a level set function.
More precisely, the idea is to represent the evolving surface position as the
set of all points
x such that the level set function
![]() (x;t) equals zero. The evolution equation takes the
form [220]
(x;t) equals zero. The evolution equation takes the
form [220]
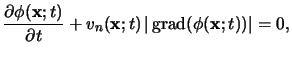 |
(7.26) |
| (7.27) |
| (7.28) |
| (7.29) |
| (7.30) |
Both partial differential equations (7.28) and (7.31) can conveniently be solved with finite-difference methods, whereby care has to be taken to adequately discretize the spatial derivatives in the gradient. A big advantage of the level set approach lies in the fact that the formulation applies to two as well as three spatial dimensions. Generally, the equations can be solved robustly and very fast. For the stationary form (7.31) an acceleration technique called fast marching technique was proposed in [221]. For example, less than one minute simulation time on a SPARC 10 workstation was reported for 200 x 200 x 200 grid points [222]. The various formulations of the level set method have found a wide application for numerous problems in lithography as well as etching and deposition [223,224,225,226]. For example, the lithography simulator DEPICT [226] and the topography simulator TERRAIN [227] rely on them. For further reading on level set methods see [228].d
Cellular algorithms. The third approach was originally proposed by Frederick Dill and relies on a cellular material representation of the underlying geometry [141]. The geometry is divided into a regular array of rectangular prismatic elements. Cells which are exposed constitute the surface. There are two different methods how to propagate the surface, namely the cell-removal algorithm [141,229,213] and the recently proposed structuring element algorithm [230,231,232,233,234]. Cellular algorithms are the most robust of all methods introduced thus far. They are relatively easy to implement in two as well as three spatial dimensions, requiring only a simple set of arrays. We will briefly describe the former algorithm and then discuss the latter one in greater detail since we have adapted it for our development module.
In the cell-removal algorithm the time for the removal of each cell depends on the local development rate and the number of exposed faces. Development proceeds along a surface consisting of unetched cells in contact with etched cells [141]. As the cells are etched away, new cells are exposed to the developer and thus added to the developer. The algorithm, however, is slow and inefficient and can require staggering amounts of computation time and memory in order to produce accurate results. The primary difficulty with the cell-removal algorithm is the trade-off between accuracy and computation time. The accuracy of the simulation increases as the cell-size is decreased, but at the cost of an increased number of cells and an increased computation time. Another serious problem is facet formation. For example, in the case of a uniform isotropic etching simulation beginning from a single seed point the method produces an octagon instead of a circle [211]. This observation led to the development of the previously described string algorithm. Faceting is most probably caused by the use of nearest-neighbor square cells to represent the circular etch. It is extremely troublesome since an increase in cell density decreases the accuracy of the simulation since facets appear more quickly with distance [213]. For lithographic applications this effect is somewhat averaged out and a reasonable accuracy can be achieved [229]. The lithography simulator SOLID [106] uses this method.
The structuring element algorithm introduced in [230,231] by Ernst
Strasser et al. overcomes the shortcomings of the cell-removal algorithm.
The algorithm is based on the two fundamental morphological operations of
erosion and dilatation. These operations are well-known in digital
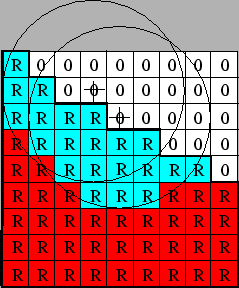
image processing [235]. The method can be implemented by moving
a filter called the structuring element along the surface. Cells within
the filter are etched away, while cells outside stay unchanged. A
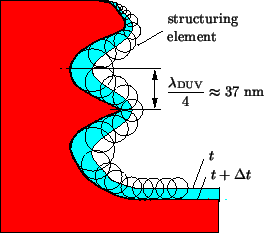
graphical illustration of this operation is shown in
Figure 7.3. Within the scope of lithography simulation
the structuring element is a circle or sphere in two and three dimensions,
respectively, since the development can be modeled as an isotropic etching
process [141]. The radius depends on the precalculated development rate
multiplied by the chosen time step. The algorithm avoids faceting errors since
the filtering implicitly suppresses them at every time step. This
is a big advantage of the structuring element algorithm over the cell-removal
algorithm. As before, accuracy and run-time depend on the number N
of cells. In three dimensions the run-time can be estimated to grow with
![]() (N3), which is two orders more efficient than with the
cell removal algorithm [234]. However, a higher cellular resolution
is required since the structuring element has to be resolved with sufficient
precision.
(N3), which is two orders more efficient than with the
cell removal algorithm [234]. However, a higher cellular resolution
is required since the structuring element has to be resolved with sufficient
precision.
|
For lithographic applications the original proposed structuring element
algorithm
has to be adapted to account for the strong spatial dependence of the
development rate. Possible sources for these variations are standing waves and
notching effects occurring during exposure. The required number of cells has to
be chosen to resolve them. For example, in the case of standing waves we know
that
the distance between the maxima and minima of the absorbed light intensity and
therefore also of the development rate is ![]() /4 yielding approximately
37 nm for DUV illumination at a wavelength
/4 yielding approximately
37 nm for DUV illumination at a wavelength ![]() =248 nm and a refractive
index of 1.65 for the photoresist (c.f. Figure 7.3). For an
accurate movement of the development front this significant distance should be
resolved by 10 cells. Hence a cell density of 300 cells/
=248 nm and a refractive
index of 1.65 for the photoresist (c.f. Figure 7.3). For an
accurate movement of the development front this significant distance should be
resolved by 10 cells. Hence a cell density of 300 cells/![]() m is
required. The applicability of the advancement algorithm for this cellular
geometry resolution has been demonstrated in [234]. The time-increment
is chosen in a way so that the structuring element for the maximal local
development rate occurring at a certain time-step comprises roughly 10 cells.
Simulation results obtained with the structuring element algorithm are presented
in Section 8.2. Exact numbers on run-time and memory demands
can also be found there.
m is
required. The applicability of the advancement algorithm for this cellular
geometry resolution has been demonstrated in [234]. The time-increment
is chosen in a way so that the structuring element for the maximal local
development rate occurring at a certain time-step comprises roughly 10 cells.
Simulation results obtained with the structuring element algorithm are presented
in Section 8.2. Exact numbers on run-time and memory demands
can also be found there.