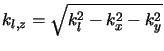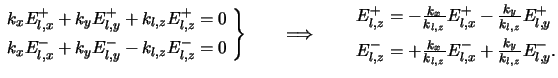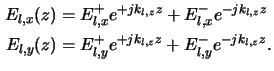Electric Field

We assume that a homogeneous plane wave coming from a certain direction k₀ = (k_x  k_y  k_{0, z})^T strikes onto a planar homogeneous layer l. Within the layer the electric field consists of two plane waves traveling in opposite directions k_l⁺ and k_l^-. This situation is schematically illustrated in Figure C.1. The electric phasor E_l(x) is thus written as

 

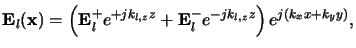$$\mathbf{E}_l(\mathbf{x}) = \left(\mathbf{E}_l^+ e^{+jk_{l,z}z} + \mathbf{E}_l^- e^{-jk_{l,z}z}\right) e^{j(k_xx+k_yy)},$$ (C.1)

whereby E_l⁺ and E_l^- are the wave amplitudes traveling downwards and upwards the layer. The two wavevectors are given by

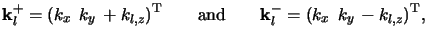$$\mathbf{k}_l^+ = (k_x \;\, k_y \, +k_{l,z})^{\mathrm{T}}{}\qquad{\text{and}}\qquad{}\mathbf{k}_l^- = (k_x \;\, k_y \, -k_{l,z})^{\mathrm{T}},$$ (C.2)

and the vertical wavevector component

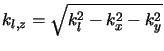$$k_{l,z} = \sqrt{k_l^2 - k_x^2 - k_y^2}$$ (C.3)

depends on the wavenumber k_l = k₀n_l of the layer material with refractive index n_l.

  

Figure C.1: In a homogeneous planar layer with refractive index n_l the electric field consists of two plane waves E_l⁺ and E_l^- traveling downwards and upwards, respectively.

Due to the transverseness of the plane waves the vertical amplitude components can be expressed by the lateral ones, i.e.,

 

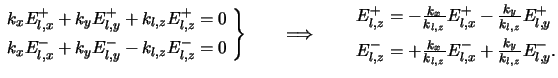$$\left.\begin{aligned}k_xE^+_{l,x} + k_yE^+_{l,y} + k_{l,z}E^+_{l,... ...yle+\frac{k_x}{k_{l,z}} E^-_{l,x} + \frac{k_y}{k_{l,z}} E^-_{l,y}.\end{aligned}$$ (C.4)

Hence it suffices to study only the lateral field components of (C.1) given by

 

$$\begin{aligned}E_{l,x}(z) &= E^+_{l,x} e^{+jk_{l,z}z} + E^-_{l,x}... ...E_{l,y}(z) &= E^+_{l,y} e^{+jk_{l,z}z} + E^-_{l,y} e^{-jk_{l,z}z}.\end{aligned}$$

In these two equations E_{l, x}(z) and E_{l, y}(z) refer to the z-dependent part of the electric field phasor. As can be seen from (C.1) the complete phasor is obtained by multiplication with the exponential factor exp(j(k_xx + k_yy)), which describes the lateral dependence.