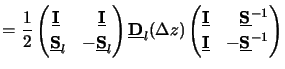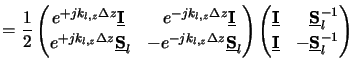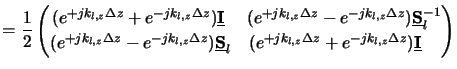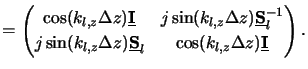Next: C.2 Stack of Homogeneous
Up: C.1 One Homogeneous Planar
Previous: Matrix Factorization
Now it is easy to find a relation like
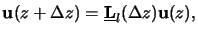 |
(C.17) |
which connects the lateral field components at two different vertical points that
are at a distance 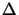 z from each other.
The matrix
z from each other.
The matrix
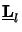 (
(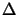 z) is called the propagation matrix
of the layer l and is obtained in the following way:
Evaluating (C.18) at the two different points gives
ul(z +
z) is called the propagation matrix
of the layer l and is obtained in the following way:
Evaluating (C.18) at the two different points gives
ul(z + 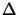 z) =
z) = 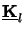
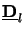 (z +
(z + 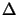 z)el and
el =
z)el and
el = 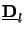 (- z)
(- z) 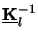 ul(z),
which combines with the second relation of (C.14) to
ul(z),
which combines with the second relation of (C.14) to
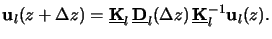 |
(C.18) |
Hence an explicit expression for the propagation matrix
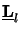 (
(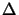 z) can be derived to
The propagation matrix has some interesting properties. For example,
in case of a vanishing distance
z) can be derived to
The propagation matrix has some interesting properties. For example,
in case of a vanishing distance
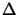 z = 0 we obtain
z = 0 we obtain
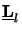 (0) =
(0) = 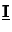 .
It can also be shown that the reciprocity relation
.
It can also be shown that the reciprocity relation
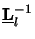 (
(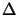 z) =
z) = 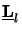 (-
(- 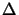 z) exists.
Additionally, in two-dimensionsa
the matrices
z) exists.
Additionally, in two-dimensionsa
the matrices
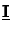 and
and
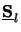 are replaced by its
determinants, i.e.,
are replaced by its
determinants, i.e.,
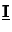
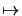 det
det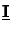 = 1 and
= 1 and
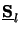
 det
det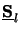 = 1/
= 1/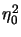 . The resulting
expression for the propagation matrix (C.21) can
be found in many textbooks, e.g., in [11, p. 58].
Finally,
. The resulting
expression for the propagation matrix (C.21) can
be found in many textbooks, e.g., in [11, p. 58].
Finally,
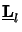 (
(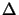 z) is a normal matrix as
z) is a normal matrix as
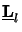 (
(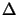 z)
z)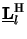 (
(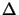 z) =
z) = 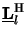 (
(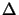 z)
z)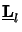 (
(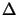 z) holds,
whereby the superscript
H denotes Hermitian or complex-conjugate transposition. This property
proves the existence of an eigenvalue decomposition. The four eigenvalues
of
z) holds,
whereby the superscript
H denotes Hermitian or complex-conjugate transposition. This property
proves the existence of an eigenvalue decomposition. The four eigenvalues
of
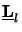 (
(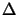 z) consist of two pairs
z) consist of two pairs 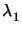 and
and 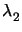 that are both of manifold two. They are inverse
as the determinant and thus their product equals unity, i.e.,
det
that are both of manifold two. They are inverse
as the determinant and thus their product equals unity, i.e.,
det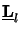 (
(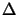 z) =
z) = 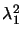
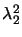 = 1.
The two values
= 1.
The two values 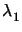 and
and 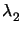 can easily be calculated and
equal to
can easily be calculated and
equal to
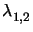 = exp(
= exp( 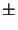 jkl, z
jkl, z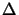 z), which correctly describes
the damping
exp(
z), which correctly describes
the damping
exp( 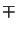 Im[kl, z]
Im[kl, z]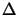 z) and the oscillation
exp(
z) and the oscillation
exp( 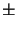 jRe[kl, z]
jRe[kl, z]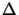 z) of the plane wave traveling upwards and
downwards the layer.
z) of the plane wave traveling upwards and
downwards the layer.
Footnotes
- ... two-dimensionsa
- A two-dimensional
analysis always suffices because the field lies
in one common plane and the coordinates can be chosen in such a way
that one lateral field vector component vanishes.
However, we present a three-dimensional analysis as the
results can directly be used as boundary conditions for the
differential method.




Next: C.2 Stack of Homogeneous
Up: C.1 One Homogeneous Planar
Previous: Matrix Factorization
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17