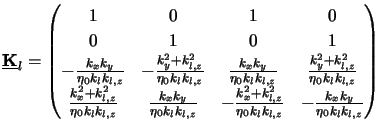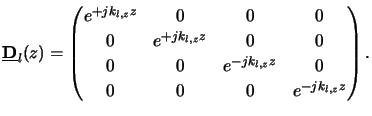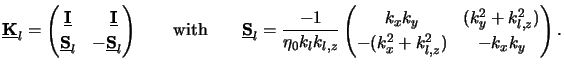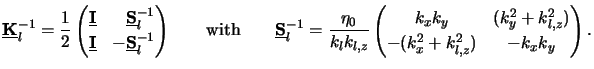Next: Propagation Matrix
Up: C.1 One Homogeneous Planar
Previous: Matrix Notation
For further investigations it is useful to split up
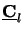 (z) into
two parts, namely into a constant matrix
(z) into
two parts, namely into a constant matrix
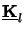 describing the
orientation of the wave propagation and into a z-dependent diagonal matrix
describing the
orientation of the wave propagation and into a z-dependent diagonal matrix
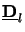 (z) representing the amplitude oscillation within the layer.
Hence we write
(z) representing the amplitude oscillation within the layer.
Hence we write
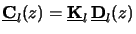 |
(C.9) |
with
Some interesting properties exist for the three matrices defined
by (C.11) to (C.13),
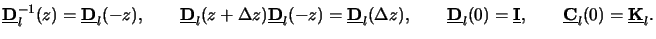 |
(C.12) |
The validity of each of these relations is self-evident. However, as they
will be used further on we explicitly summarized them in (C.14).
Additionally, the orientation matrix
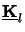 defined in
(C.12) can be factorized as follows:
defined in
(C.12) can be factorized as follows:
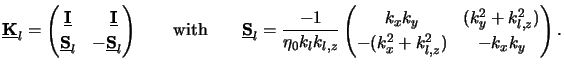 |
(C.13) |
Finally, the inverse matrix
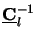 (z) of
(z) of
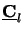 (z)
is of interest. From (C.11) and (C.13) we obtain
with (C.14)
(z)
is of interest. From (C.11) and (C.13) we obtain
with (C.14)
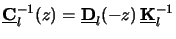 |
(C.14) |
whereby
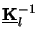 is given by
is given by
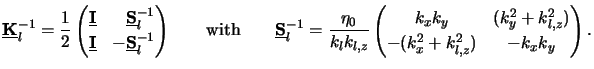 |
(C.15) |
Note that
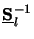 simply equals to
simply equals to
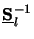 = - 1/
= - 1/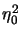
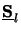 .
.
Summarizing the results of the matrix notation and factorization
(cf. (C.10), (C.11) and (C.16))
shows that the lateral field components
ul(z) are related to
the electric amplitudes
el by
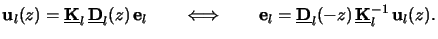 |
(C.16) |




Next: Propagation Matrix
Up: C.1 One Homogeneous Planar
Previous: Matrix Notation
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17