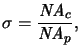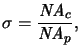Next: 2.4 Photomask
Up: 2.3 Illuminator
Previous: 2.3.2 Condenser Lens
2.3.3 Partial Coherence and Advanced Apertures
Two aspects of coherence play an important role in lithography. Firstly,
the light is strongly coherent in the time domain because of the required
monochromaticity of the light source (cf. Section 2.3.1).
The coherence in the spatial domain, however, is an adjustable parameter
that has great influence on the imaging performance. The illumination
is said to be partially coherent, if a certain amount of spatial coherence
exists. The amount of partial coherence is governed by the ratio of the
numerical aperture of the condenser lens
NAc and projection lens
NAp
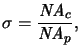 |
(2.4) |
whereby 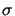 is the so-called partial coherence factor.
The influence of
is the so-called partial coherence factor.
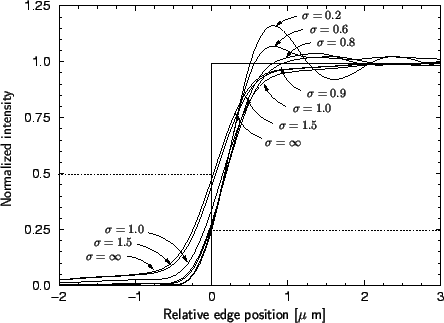
The influence of 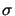 is demonstrated in Figure 2.5
by showing the image intensity near a simple knife-edge.
The limiting case
is demonstrated in Figure 2.5
by showing the image intensity near a simple knife-edge.
The limiting case
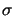 =
= 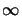 corresponds to incoherent
illumination and gives the smoothest profile.
Decreasing
corresponds to incoherent
illumination and gives the smoothest profile.
Decreasing 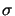 increases the edge slope
and ``overshoot'' while decreasing the intensity minimum near the edge.
This minimum determines linewidth
fidelity and profile quality. If
increases the edge slope
and ``overshoot'' while decreasing the intensity minimum near the edge.
This minimum determines linewidth
fidelity and profile quality. If 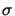 is further reduced to values as low as
0.2 in order
to decrease the intensity minimum, the overshoot becomes excessive and
extends laterally indicating that proximity effects between adjacent features
are likely. The limiting case
is further reduced to values as low as
0.2 in order
to decrease the intensity minimum, the overshoot becomes excessive and
extends laterally indicating that proximity effects between adjacent features
are likely. The limiting case 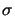 = 0 refers to an ideally
coherent point source yielding the sharpest slope but intolerable overshoot.
In practical lithography typical values for
= 0 refers to an ideally
coherent point source yielding the sharpest slope but intolerable overshoot.
In practical lithography typical values for 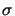 range between 0.4-0.7.
range between 0.4-0.7.
Figure 2.5:
The degree
of partial coherence 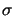 determines the tradeoff between a sharp slope and a low
overshoot (after [15]). Optimal values lie between 0.4-0.7.
determines the tradeoff between a sharp slope and a low
overshoot (after [15]). Optimal values lie between 0.4-0.7.
|
|
Further improvement can be achieved by introducing an aperture between
the light source and the condenser lens (cf. Figure 2.4).
This aperture acts as a wavefront filter. A circular aperture
as in the case of partial coherence refers to a simple low pass filtering
with cut-off frequency determined by the numerical aperture of the
condenser lens
NAc. Only plane waves up to a certain amount of
obliqueness can travel towards
the mask. Introducing an annular or quadrupole aperture blocks vertical
or zero-order waves that carry no information. The image resolution is enhanced
via the k1 parameter of (2.1) and therefore does not
decrease the depth of focus (cf. (2.2)).
For that reason such modified illumination
schemes or ``off-axis'' techniques have become a well-established
method to extend optical lithography towards sub-wavelength resolution.
A detailed description of the operation principle will be
given in the context of aerial image simulation in Chapter 4.




Next: 2.4 Photomask
Up: 2.3 Illuminator
Previous: 2.3.2 Condenser Lens
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17