



Next: 5.2.4 Beam Propagation Method
Up: 5.2 Field Calculation over
Previous: 5.2.2 Scaled Defocus Method
5.2.3 Transfer Matrix Method
The transfer matrix method overcomes the direction independence by assuming that
the light consists of various plane waves traveling with oblique angles through
the resist. The method is a straight-forward implementation of the formalism
derived in Appendix C for the analysis of a stratified
medium [11, pp. 51-70]. For lithography simulation this approach
was first proposed by Chris Mack [145] and
Douglas Bernard [103]. The transfer matrix method is also called
high-
NA scalar model and is implemented in many commercially
available lithography simulators like DEPICT [103],
PROLITH [145], and SOLID [106] as advanced
aerial image module. The basic operation principle is described as follows.
The incoming light Ui(x, y) is represented by a superposition of plane waves,
i.e.,
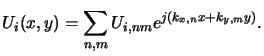 |
(5.27) |
The latent bulk image
Ur, nm(z;tk) is obtained by first calculating the
vertical amplitude dependence of the field resulting from the excitation with
one plane wave of amplitude Ui, nm,
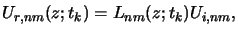 |
(5.28) |
and then reconstructing the field itself according to
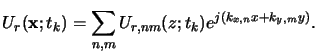 |
(5.29) |
A more detailed description is given in Appendix C on
page ![[*]](cross_ref_motif.gif) . Using the vector version of both the aerial
image tool and the transfer matrix algorithm an arbitrarily polarized
light can be simulated. Additionally, advanced apertures can be simulated
with Abbe's method. However, there are two fundamental restrictions
of this approach. Firstly the bleaching of the resist is not simulated
correctly as the layers forming the resist have to be homogeneous in lateral
direction, and secondly only imaging over a planar substrate can be modeled.
. Using the vector version of both the aerial
image tool and the transfer matrix algorithm an arbitrarily polarized
light can be simulated. Additionally, advanced apertures can be simulated
with Abbe's method. However, there are two fundamental restrictions
of this approach. Firstly the bleaching of the resist is not simulated
correctly as the layers forming the resist have to be homogeneous in lateral
direction, and secondly only imaging over a planar substrate can be modeled.




Next: 5.2.4 Beam Propagation Method
Up: 5.2 Field Calculation over
Previous: 5.2.2 Scaled Defocus Method
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
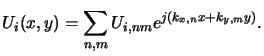
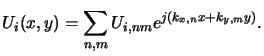
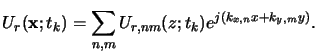
![[*]](cross_ref_motif.gif) . Using the vector version of both the aerial
image tool and the transfer matrix algorithm an arbitrarily polarized
light can be simulated. Additionally, advanced apertures can be simulated
with Abbe's method. However, there are two fundamental restrictions
of this approach. Firstly the bleaching of the resist is not simulated
correctly as the layers forming the resist have to be homogeneous in lateral
direction, and secondly only imaging over a planar substrate can be modeled.
. Using the vector version of both the aerial
image tool and the transfer matrix algorithm an arbitrarily polarized
light can be simulated. Additionally, advanced apertures can be simulated
with Abbe's method. However, there are two fundamental restrictions
of this approach. Firstly the bleaching of the resist is not simulated
correctly as the layers forming the resist have to be homogeneous in lateral
direction, and secondly only imaging over a planar substrate can be modeled.