



Next: 5.2.3 Transfer Matrix Method
Up: 5.2 Field Calculation over
Previous: 5.2.1 Vertical Propagation Method
The first attempt to correct the deficiencies of the vertical
propagation method was made by Douglas Bernard [102] and,
independently, by Chris Mack [143]. They took the
continuous change of the aerial image while propagating through
the resist into account. For example, even in air, the aerial image
depends on the vertical position with respect to the Gaussian focal plane
(cf. Section 4.2.1). Denoting the focus offset in air
by z0 and z as the position within the resist, the refractive effect of
the air/resist interface can then be described to first-order by the net
defocus
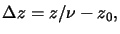 |
(5.25) |
whereby 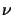 is the real part of the refractive index
n(x;tk) of the
resist (cf. (5.20)).b The aerial image is now
calculated
for the net defocus
is the real part of the refractive index
n(x;tk) of the
resist (cf. (5.20)).b The aerial image is now
calculated
for the net defocus 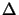 z and then multiplied with the standing wave
intensity
Ir(z;tk) to obtain the bulk intensity
I(x;tk), i.e.,
z and then multiplied with the standing wave
intensity
Ir(z;tk) to obtain the bulk intensity
I(x;tk), i.e.,
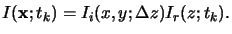 |
(5.26) |
For the calculation of
Ir(z;tk) the same methods as for the
vertical propagation model can be applied. The scaled defocus
method is nowadays the default exposure model of many lithography simulators,
e.g., PROLITH [143], SOLID [144], and SPESA [102].
However, because of the separation approach the dependence of the reflection
and refraction on the angle of incidence is again neglected. Thus the
scaled defocus method is also restricted to low numerical apertures.
Footnotes
- ...)).b
- Note that in air the refractive
index has a real part of unity, i.e.,
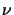 = 1.
= 1.




Next: 5.2.3 Transfer Matrix Method
Up: 5.2 Field Calculation over
Previous: 5.2.1 Vertical Propagation Method
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17