



Next: 5.3 Field Calculation over
Up: 5.2 Field Calculation over
Previous: 5.2.3 Transfer Matrix Method
A totally different method was incorporated by Andreas Erdmann into
the lithography simulator SOLID [144,146,147].
As this approach is based on the finite-difference beam propagation
method [148] it is not restricted to laterally homogeneous resists.
However, it is only suited for a planar topography. The field calculation is
based on a numerical solution of the Helmholtz equation
(cf. (4.2)) that writes inside the inhomogeneous resist as
![$\displaystyle \left[\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial z^2} + k_0^2 n^2(\mathbf{x};t_k)\right] E_{y,k}(x,z) = 0,$](img796.gif) |
(5.30) |
whereby a transversal-electric polarized light and a two-dimensional simulation
domain is required [144]. The field amplitude
Ey, k(x, z) is
separated into a slowly varying amplitude Ak(x, z) obeying
(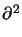 /
/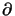 z2)Ak(x, z) = 0 and
an exponential factor
exp(
z2)Ak(x, z) = 0 and
an exponential factor
exp( 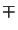 jk0
jk0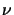 z) describing the propagation upwards
and downwards the resist, i.e.,
z) describing the propagation upwards
and downwards the resist, i.e.,
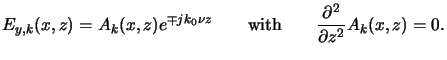 |
(5.31) |
Insertion of (5.32) into (5.31)
transforms the Helmholtz equation into
![$\displaystyle \left[\frac{\partial^2}{\partial x^2} + k_0^2 \left(n^2(\mathbf{x...
...u^2\right)\right] A_k(x,z) = \pm 2jk_0\nu \frac{\partial}{\partial z} A_k(x,z),$](img802.gif) |
(5.32) |
which for example can be solved on an equidistant grid with a Crank-Nicholson
scheme [144]. The boundary conditions can either be
transparent ones [149] used in case of isolated features, or periodic
ones applied for dense lines and spaces.
Consideration of reflective substrates requires
additional modifications as either downward or upward propagation--but not
simultaneously--can be modeled by (5.32).
However, reflections occurring at the air/resist
as well as the resist/substrate interface can conveniently be calculated by
Fresnel's reflection formulae [11, pp. 36-51].
The light is then repeatedly propagated down and up through the resist until its
intensity is negligible or, alternatively, until a fixed number of iterations
is performed and then simpler methods, e.g., the transfer matrix algorithm,
are employed.
In the above described form the beam propagation is only suited for
low-
NA applications as the beams are assumed to travel almost
parallel to the vertical axis. An extended wide angle algorithm
exists [150] that is suited for higher numerical aperture lithography
simulation. Numerical problems such as poor convergence and instability of the
solution occur in case of a strongly varying refractive index.
A more rigorous finite-difference time domain propagation method is then
required [151]. The main limitation of this method is its restriction
to planar layers. In the next section we describe various methods suited
for nonplanar topography.




Next: 5.3 Field Calculation over
Up: 5.2 Field Calculation over
Previous: 5.2.3 Transfer Matrix Method
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
![$\displaystyle \left[\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial z^2} + k_0^2 n^2(\mathbf{x};t_k)\right] E_{y,k}(x,z) = 0,$](img796.gif)
![$\displaystyle \left[\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial z^2} + k_0^2 n^2(\mathbf{x};t_k)\right] E_{y,k}(x,z) = 0,$](img796.gif)
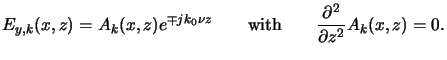
![$\displaystyle \left[\frac{\partial^2}{\partial x^2} + k_0^2 \left(n^2(\mathbf{x...
...u^2\right)\right] A_k(x,z) = \pm 2jk_0\nu \frac{\partial}{\partial z} A_k(x,z),$](img802.gif)