| Method |
Features |
Storage |
CPU |
Availability |
|
Spectral-element |
Sparse matrix, direct solution |
n5
n3 |
n7
n4 |
(Philips/Signetics, 2D) |
Time-domain
finite-difference |
Massively parallel |
n3
n2 |
n3 x 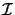
n2 x 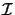 |
TEMPEST
(UC Berkeley, 2D&3D) |
|
Waveguide |
Small refractive index changes |
n4
n2 |
n6 x 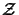
n3 x 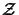 |
METROPOLE
(Carnegie-Mellon, 2D&3D) |
|
Differential |
Smooth topography |
n4
n2 |
n6 x 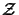
n3 x 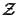 |
iPHOTO (Intel, 2D)
LISI (TU Vienna, 3D) |
Physical-optics &
fast multipole |
Piecewise linear topography |
n2
n |
n3
n1.5 |
(UC Berkeley, 3D) |
Integral &
fast multipole |
Iterative solution |
n2
n |
n3.3 x 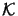
n1.5 x 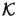 |
(UC Berkeley, 3D) |
Upper quantities characterize the storage and computational costs
for three-dimensional simulations, whereas lower quantities
refer to two-dimensions. The symbols
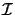 and and
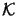 signify the number of iterations required for the
respective technique, and signify the number of iterations required for the
respective technique, and
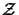 denotes the accuracy
of the vertical discretization. denotes the accuracy
of the vertical discretization.
|