



Next: 4.1.2 Phase Transformation Properties
Up: 4.1 Principles of Fourier
Previous: 4.1 Principles of Fourier
Light is an electromagnetic wave with coupled electric and magnetic fields
traveling through space. In a homogeneous isotropic medium, like free space
or a lens with constant refractive index, the electric and magnetic
field vectors form a right-handed orthogonal triad with the direction of
propagation. Disregarding polarization, the field can be described
by a scalar function
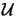 (x;t) representing either the
electric or the magnetic field amplitude. As the light used in microlithography
exhibits a strong monochromacity (cf. Section 2.3.1) the time
dependence of the field is a harmonic one and can thus be explicitly written as
(x;t) representing either the
electric or the magnetic field amplitude. As the light used in microlithography
exhibits a strong monochromacity (cf. Section 2.3.1) the time
dependence of the field is a harmonic one and can thus be explicitly written as
![$\displaystyle \mathcal{U}(\mathbf{x}; t) = \operatorname{Re}\left[U(\mathbf{x})e^{-j\omega t}\right].$](img282.gif) |
(4.1) |
Here, 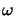 denotes the angular frequency of the light, and the
complex-valued amplitude or phasor
U(x) depends on the
spatial coordinates
x = (x y z)T only. If
both quantities
denotes the angular frequency of the light, and the
complex-valued amplitude or phasor
U(x) depends on the
spatial coordinates
x = (x y z)T only. If
both quantities
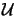 (x;t) and
U(x) represent
an optical wave, they must satisfy the
Helmholtz equationa
(x;t) and
U(x) represent
an optical wave, they must satisfy the
Helmholtz equationa
![$\displaystyle \left[ \triangle - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} ...
...qquad{\text{and}}\qquad\quad{}\left[ \triangle + k^2 \right] U(\mathbf{x}) = 0.$](img290.gif) |
(4.2) |
The Helmholtz equation directly follows from the Maxwell equations
under the condition of a homogeneous medium and in absence of sources.
The quantity
k is termed the wavenumber or propagation constant of the medium and
is related to the light velocity c, the angular frequency 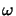 , and
the vacuum wavelength
, and
the vacuum wavelength 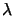 byb
byb
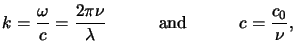 |
(4.3) |
whereby 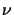 is the refractive index of the medium, e.g., in vacuum
is the refractive index of the medium, e.g., in vacuum
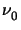 = 1.
= 1.
The complex disturbance
U(x) at any observation point
xo in space can be computed from the Helmholtz
equation (4.2) with the help of
Green's theorem.c If a unit-amplitude spherical wave expanding
about the observation point
x0 is chosen as Green's function, i.e.,
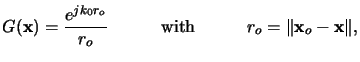 |
(4.4) |
the so-called integral theorem of Helmholtz and Kirchhoff is
obtained [11, p. 377]:
![$\displaystyle U(\mathbf{x}_o) = -\frac{1}{4\pi} \iint\limits_\mathcal{S}\left[ ...
...athbf{x}) - U(\mathbf{x}) \frac{\partial G(\mathbf{x})}{\partial n} \right] ds.$](img303.gif) |
(4.5) |
This relation plays a central role in the derivation of the scalar theory
of diffraction, for it allows the field
U(x) at an observation point
xo to be expressed in terms of the ``boundary values''
on any closed surface
 surrounding
xo.
surrounding
xo.
The integral theorem of (4.5)
can readily be used to study diffraction effects occurring at
a plane object. Therefore the integration surface
 is segmented
into three disjoint parts, i.e.,
is segmented
into three disjoint parts, i.e.,
 =
= 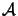
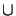
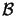
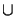
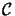 .
The boundary
.
The boundary
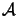 is chosen across the object location in the screen
plane,
is chosen across the object location in the screen
plane,
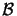 is the opaque part of the screen, and
is the opaque part of the screen, and
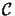 is a half-sphere containing the observation point
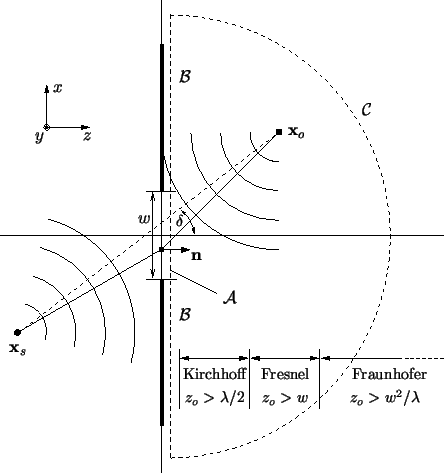
xo. A graphical illustration of this specific choice is given
in Figure 4.1. The solution of the diffraction problem
is found by specifying Kirchhoff boundary conditions on
is a half-sphere containing the observation point
xo. A graphical illustration of this specific choice is given
in Figure 4.1. The solution of the diffraction problem
is found by specifying Kirchhoff boundary conditions on
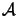 and
and
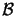 , and the Sommerfeld radiation condition
on
, and the Sommerfeld radiation condition
on
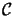 :
:
whereby
Us(x) is the field incident on the
screen. The Kirchhoff boundary conditions are an idealization
to the real field distribution on the screen by assuming that the field
and its derivative across
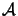 is exactly
the same as they would be in the absence of the screen.
In the geometrical shadow across
is exactly
the same as they would be in the absence of the screen.
In the geometrical shadow across
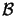 the field is simply set to zero.
Although these assumptions are reasonable, they fail in the immediate
neighborhood of the rim of the opening. Thus, the range of validity is
related to the wavelength
the field is simply set to zero.
Although these assumptions are reasonable, they fail in the immediate
neighborhood of the rim of the opening. Thus, the range of validity is
related to the wavelength 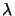 and the geometrical dimension w of the
opening (cf. Figure 4.1). The Sommerfeld radiation condition
on
and the geometrical dimension w of the
opening (cf. Figure 4.1). The Sommerfeld radiation condition
on
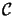 is satisfied, if the disturbance
U(x)
vanishes at least as fast
as a spherical wave. Since the illuminating light
Us(x)
invariably consists of a
linear combination of spherical waves, this requirement is always fulfilled.
is satisfied, if the disturbance
U(x)
vanishes at least as fast
as a spherical wave. Since the illuminating light
Us(x)
invariably consists of a
linear combination of spherical waves, this requirement is always fulfilled.
Figure 4.1:
Range of validity
of scalar diffraction theories. Depending on the distance zo between
observation point
xo and screen,
several approximations can be
employed to describe diffraction. For aerial image simulation the
far-field theory of Fraunhofer valid for
zo 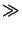 w2/
w2/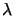 is
adequate since in M : 1-reduction projection systems the patterns to
be imaged are of size
w
is
adequate since in M : 1-reduction projection systems the patterns to
be imaged are of size
w 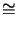 M
M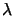 and we thus get
zo
and we thus get
zo 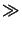 M2
M2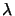
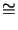 0.1 mm for M = 10 and
0.1 mm for M = 10 and
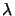
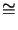 400 nm.
400 nm.
|
|
Inserting the boundary conditions of (4.6) into
the integral theorem (4.5) shows that only the
illuminating light
Us(x) across the opening
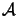 contributes to the
integral, i.e.,
contributes to the
integral, i.e.,
![$\displaystyle U(\mathbf{x}_o) = -\frac{1}{4\pi} \iint\limits_\mathcal{A}\left[ ...
...hbf{x}) - U_s(\mathbf{x}) \frac{\partial G(\mathbf{x})}{\partial n} \right] ds.$](img334.gif) |
(4.6) |
We further assume that the aperture is illuminated with a single expanding
spherical wave arising from a point source located in
xs,
a distance rs away from the screen (cf. Figure 4.1),
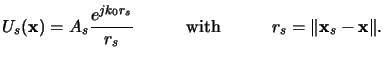 |
(4.7) |
Hence, both Green's function in (4.4) and the incident
disturbance in (4.8) have the shape of spherical waves.
A further simplification is
obtained by noting that the distances from the screen to the observation
point and
the location of the point source, ro and rs, respectively, are
many optical wavelengths. Therefore the following
approximations hold for
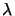
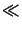 ro, rs:d
ro, rs:d
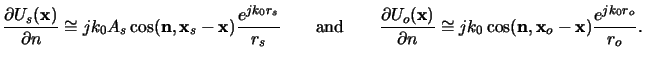 |
(4.8) |
Insertion of these approximations into (4.7)
yields together with (4.4) and (4.8)
the Fresnel-Kirchhoff diffraction formula
![$\displaystyle U(\mathbf{x}_o) = \frac{jA_s}{\lambda} \iint\limits_\mathcal{A}\f...
...bf{x}_o-\mathbf{x}) - \cos(\mathbf{n},\mathbf{x}_s-\mathbf{x})}{2} \right]\,ds.$](img348.gif) |
(4.9) |
The term in square brackets is called obliquity or inclination factor and
was first introduced by Fresnel based on heuristic arguments,
when he combined Huygens'
envelope construction with Young's principle of interference. The mathematical
sound derivation described above was later developed by Kirchhoff.
An interesting property of the diffraction formula (4.10)
is its symmetry with respect to the source
and observation point, a result that is sometimes referred to as the
reciprocity theorem of Helmholtz.
For our purposes we rewrite (4.10) by introducing
a general linear relationship between the exciting field Us(x, y)
at the screen and the resulting
diffraction pattern
U(xo, yo)e
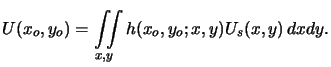 |
(4.10) |
Note that we are always interested in field values lying in certain
planes parallel to the screen. Therefore, only the dependence on the
lateral x- and y-coordinate is explicitly written, whereas the vertical
position is indicated by subscripts.
The integration kernel
h(x, y;xo, yo) of the superposition integral
in (4.11) is given by (cf. (4.8)
and (4.10))
![$\displaystyle h(x_o,y_o;x,y) = \frac{j}{\lambda} \left[\frac{\cos(\mathbf{n},\m...
... - \cos(\mathbf{n},\mathbf{x}_s-\mathbf{x})}{2}\right] \frac{e^{jk_0r_o}}{r_o}.$](img352.gif) |
(4.11) |
Depending on the distance zo between the observation point
xo and the screen, the kernel
h(xo, yo;x, y) can be simplified.
The denominator ro is approximated by
zo provided that zo is much larger than the lateral extent w
of the object. For the same reason and by assuming that the source as well as
the observation point are located near the optical axis, the inclination factor
is approximately given by
cos (cf. Appendix A).
As shown in Figure 4.1
the angle
(cf. Appendix A).
As shown in Figure 4.1
the angle  lies between the line from source to observation point
and the normal vector
n.
The approximation of the exponential factor is more involved,
since ro is multiplied by the very large wavenumber k0.
Hence, a truncation of Taylor series expansions is employed,
lies between the line from source to observation point
and the normal vector
n.
The approximation of the exponential factor is more involved,
since ro is multiplied by the very large wavenumber k0.
Hence, a truncation of Taylor series expansions is employed,
- Fresnel approximations are obtained by truncating the Taylor
series after the first term, i.e.,
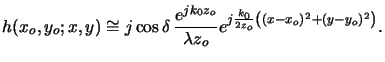 |
(4.12) |
The resulting integral relation (4.11) involves Fresnel's
integrals.f Due to
the square dependence on the integration variables (x, y),
no analytical solution exists. Tabulated values can be found in,
e.g., [115, ch. 7].
The approximation (4.14) holds for
(2zo)3 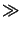 k0[(x - xo)2 + (y - yo)2]2max or simply zo
k0[(x - xo)2 + (y - yo)2]2max or simply zo 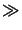 w.
w.
- Fraunhofer approximations additionally neglect the square
dependence on the integration variables (x, y) resulting in
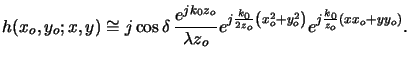 |
(4.13) |
The integral relation (4.11) corresponds now to a
Fourier transform, i.e., the dependence on the integration variables
is a linear one. Efficient numerical techniques
like FFT can be used for evaluation. The range of validity
of (4.15) is given by
2zo 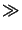 k(x2 + y2)max or
z
k(x2 + y2)max or
z 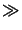 w2/
w2/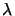 .
.
Footnotes
- ... a
- The symbol
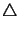 denotes the
Laplace operator, i.e.,
denotes the
Laplace operator, i.e.,
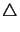 =
= 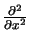 +
+ 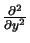 +
+ 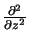 .
.
- ... byb
- The quantity c0 is the vacuum
light velocity and has a value of
c0
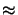 2.998 108 m/s.
2.998 108 m/s.
- ... theorem.c
- Green's theorem states that if a complex-valued
function
U(x) is continuous and has continuous single-valued first
and second partial derivatives inside a volume
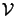 surrounded by a
closed surface
surrounded by a
closed surface
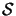 , the following relation holds:
, the following relation holds:
![\begin{displaymath}\iiint\limits_{\mathcal{V}}
[G(\mathbf{x})\triangle U(\mathb...
...mathbf{x})\frac{\partial G(\mathbf{x})}{\partial n} \right]ds,
\end{displaymath}](img299.gif) whereby the so-called Green's function
G(x) is any other function
with the same continuity requirements as
U(x) and
whereby the so-called Green's function
G(x) is any other function
with the same continuity requirements as
U(x) and
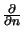 = n . grad
signifies a partial derivative in
the inward normal direction
n at each point on
= n . grad
signifies a partial derivative in
the inward normal direction
n at each point on
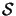 .
.
- ...:d
- For
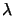
 r and
thus
1/r
r and
thus
1/r  k0 we get
k0 we get
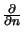
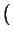 ejk0r/r
ejk0r/r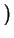 = cos(n, x)
= cos(n, x)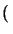 jk0 - 1/r
jk0 - 1/r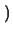 ejk0r/r
ejk0r/r 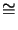 jk0cos(n, x)ejk0r/r.
jk0cos(n, x)ejk0r/r.
- ...)e
- All integrations and sums
go from -
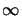 to
to 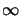 unless specified otherwise.
unless specified otherwise.
- ...
integrals.f
- Integrals of the type
C(w) =
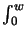 cos(
cos(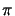
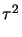 /2) d
/2) d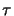 and
S(w) =
and
S(w) = 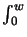 sin(
sin(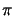
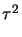 /2) d
/2) d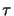 are referred to as Fresnel's integrals [115, ch. 7].
are referred to as Fresnel's integrals [115, ch. 7].




Next: 4.1.2 Phase Transformation Properties
Up: 4.1 Principles of Fourier
Previous: 4.1 Principles of Fourier
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
![$\displaystyle \left[ \triangle - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} ...
...qquad{\text{and}}\qquad\quad{}\left[ \triangle + k^2 \right] U(\mathbf{x}) = 0.$](img290.gif)
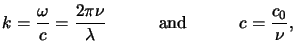
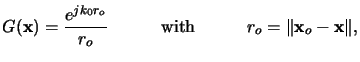
![$\displaystyle U(\mathbf{x}_o) = -\frac{1}{4\pi} \iint\limits_\mathcal{S}\left[ ...
...athbf{x}) - U(\mathbf{x}) \frac{\partial G(\mathbf{x})}{\partial n} \right] ds.$](img303.gif)
![]() is segmented
into three disjoint parts, i.e.,
is segmented
into three disjoint parts, i.e.,
![]() =
= ![]()
![]()
![]()
![]()
![]() .
The boundary
.
The boundary
![]() is chosen across the object location in the screen
plane,
is chosen across the object location in the screen
plane,
![]() is the opaque part of the screen, and
is the opaque part of the screen, and
![]() is a half-sphere containing the observation point
xo. A graphical illustration of this specific choice is given
in Figure 4.1. The solution of the diffraction problem
is found by specifying Kirchhoff boundary conditions on
is a half-sphere containing the observation point
xo. A graphical illustration of this specific choice is given
in Figure 4.1. The solution of the diffraction problem
is found by specifying Kirchhoff boundary conditions on
![]() and
and
![]() , and the Sommerfeld radiation condition
on
, and the Sommerfeld radiation condition
on
![]() :
:
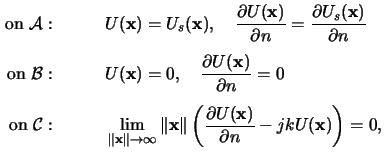
![]() contributes to the
integral, i.e.,
contributes to the
integral, i.e.,
![$\displaystyle U(\mathbf{x}_o) = -\frac{1}{4\pi} \iint\limits_\mathcal{A}\left[ ...
...hbf{x}) - U_s(\mathbf{x}) \frac{\partial G(\mathbf{x})}{\partial n} \right] ds.$](img334.gif)
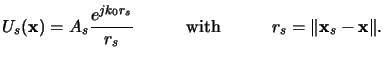
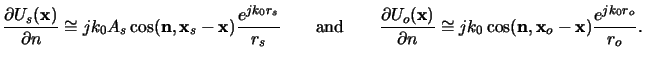
![$\displaystyle U(\mathbf{x}_o) = \frac{jA_s}{\lambda} \iint\limits_\mathcal{A}\f...
...bf{x}_o-\mathbf{x}) - \cos(\mathbf{n},\mathbf{x}_s-\mathbf{x})}{2} \right]\,ds.$](img348.gif)
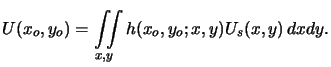
![$\displaystyle h(x_o,y_o;x,y) = \frac{j}{\lambda} \left[\frac{\cos(\mathbf{n},\m...
... - \cos(\mathbf{n},\mathbf{x}_s-\mathbf{x})}{2}\right] \frac{e^{jk_0r_o}}{r_o}.$](img352.gif)
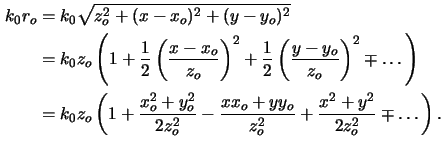
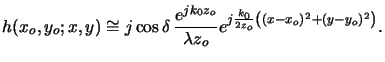
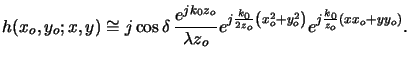
![\begin{displaymath}\iiint\limits_{\mathcal{V}}
[G(\mathbf{x})\triangle U(\mathb...
...mathbf{x})\frac{\partial G(\mathbf{x})}{\partial n} \right]ds,
\end{displaymath}](img299.gif) whereby the so-called Green's function
G(x) is any other function
with the same continuity requirements as
U(x) and
whereby the so-called Green's function
G(x) is any other function
with the same continuity requirements as
U(x) and