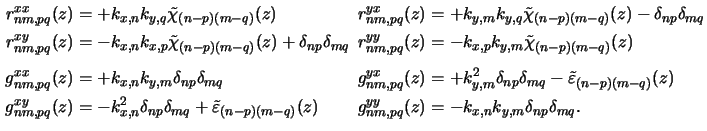


Next: 6.2.5 Truncation of the
Up: 6.2 Lateral Discretization of
Previous: 6.2.3 Elimination of the
A simple scaling yields a more compact form for the ODE
system (6.19). An appropriate choice is
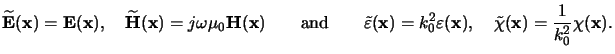 |
(6.14) |
By introducing the Kronecker symbolb
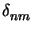 the
ODEs write to
whereby the coefficients are given by
the
ODEs write to
whereby the coefficients are given by
Footnotes
- ... symbolb
- The Kronecker symbol is defined as
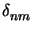 = 1 for n = m and 0 otherwise.
= 1 for n = m and 0 otherwise.
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
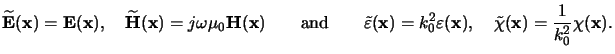
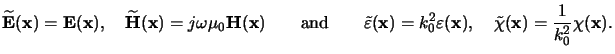
![$\displaystyle \begin{aligned}\frac{d \widetilde{E}_{x,nm}(z)}{d z} &= \sum_{p,q...
...de{E}_{x,pq}(z) + g_{nm,pq}^{yy}(z)\widetilde{E}_{y,pq}(z)\right],\end{aligned}$](img849.gif)