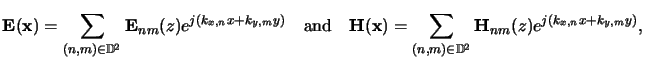Next: 6.2.6 Vector-Matrix Notation
Up: 6.2 Lateral Discretization of
Previous: 6.2.4 Scaling of the
6.2.5 Truncation of the Fourier expansions
Note that up to now no approximations have been performed. We only inserted
Fourier expansions into the Maxwell equations and thereby transformed the
PDEs into ordinary ones. This means that the
frequency domain formulation of (6.21) is totally equivalent to
the spatial domain formulation of (6.5) provided, of course,
that the EM field is laterally periodic. However, the rank of the
ODE (6.21) is generally infinite, i.e., the dependence on the
continuous spatial coordinates is transformed into an infinite number of
Fourier coefficients. Only in case of homogeneous planar layers a finite number
of Fourier coefficients suffices, i.e., those coefficients which are excited by
the incident waves (cf. Appendix C).
For a laterally constant permittivity, i.e.,
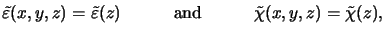 |
(6.15) |
the ODE coefficients of (6.22) have only diagonal entries since
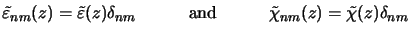 |
(6.16) |
holds in this case. EM scattering due to material inhomogeneity or the
nonplanar material
interfaces causes a coupling of all Fourier coefficients. The incident
modes thus excite other, higher-order modes. The coupling degree is
determined by the strength of the inhomogeneity or, in other words, by the
number of the relevant Fourier coefficients
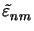 (z) and
(z) and
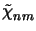 (z) of the permittivity and its reciprocal, respectively.
These basic considerations are helpful for the next step in the overall
discretization procedure, namely the truncation of the Fourier expansions
of the lateral field components.
(z) of the permittivity and its reciprocal, respectively.
These basic considerations are helpful for the next step in the overall
discretization procedure, namely the truncation of the Fourier expansions
of the lateral field components.
The EM field inside the resist and wafer is excited by the diffraction orders
collected by the projection lens (cf. 4.1). The number of
plane waves traveling towards the resist is determined by the pupil function
that is in fact a low-pass function (cf. (4.53)
or (4.58)). Thus only low-order Fourier coefficients
are directly excited by the incoming light, higher-order coefficients are
indirectly stimulated by scattering effects. Hence we have to choose the
truncation frequencies Nx and Ny higher than the cut-off frequencies of
the projection lens. The exact values have to be chosen accordingly to catch
enough coefficients so that scattering effects can be treated with sufficient
precision. In the practical implementation the two cut-off frequencies Nx
and Ny are input arguments to the simulator and it is the user's
responsibility to choose them appropriately. Easy guidelines are given below,
whereas an analysis of important implications due to the truncation
can be found in Appendix D, where a lateral stepped permittivity
as occurring at a nonplanar material interface is discussed.
The mathematical formulation of the truncation process writes as follows: Only
coefficients symmetrically centered around the vertical incident ray n = m = 0 are
considered, i.e., the index pair (n, m) must be an element of the set
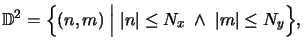 |
(6.17) |
whereas field coefficients not contained in
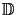 2 are set to zero, i.e,
2 are set to zero, i.e,
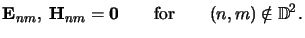 |
(6.18) |
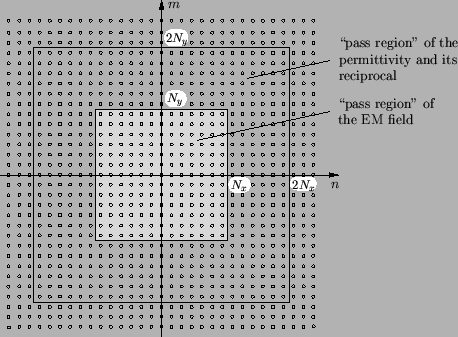
This situation is graphically illustrated in Figure 6.3.
Generally the real values of the neglected coefficients
(n, m)
 2 will not vanish. Hence also the considered
coefficients
(n, m)
2 will not vanish. Hence also the considered
coefficients
(n, m) 
 2 are only calculated approximately since
they also depend on the neglected ones due to the convolution-like relations
in (6.19). Thus the approximations made throughout the truncation
of the field expansions,
2 are only calculated approximately since
they also depend on the neglected ones due to the convolution-like relations
in (6.19). Thus the approximations made throughout the truncation
of the field expansions,
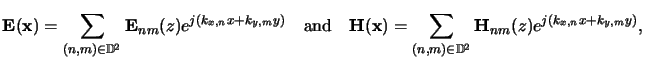 |
(6.19) |
entail two important implications:
- 1.
- A low-pass filtering of the field.
- 2.
- A low-pass filtering of the geometry.
The first is obvious and can directly be seen from the truncated
series (6.27);
the second, however, is somewhat more complicated. Namely, the medium is
treated as if it were so smooth that no coupling to higher-order
modes occurs (cf. (6.26)). Of course, this assumption is
only true for small variations of the refractive index or, similarly, for
smooth topography. Note that this limitation also applies to the second
frequency domain method of the waveguide model
(cf. Table 5.1) and is implicitly contained in any
spectral method.
The Fourier coefficients of the permittivity
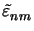 (z) and its
reciprocal
(z) and its
reciprocal
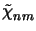 (z), on the other hand, can be exactly computed.
Because of the truncation of the field expansions and due
to the convolution-like relations in (6.19) it suffices to
calculate coefficients
(z), on the other hand, can be exactly computed.
Because of the truncation of the field expansions and due
to the convolution-like relations in (6.19) it suffices to
calculate coefficients
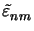 (z) and
(z) and
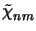 (z)
up to an order of
(z)
up to an order of
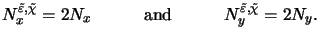 |
(6.20) |
Hence, roughly twice as many coefficients of the permittivity and its
reciprocal as of the field are required. These relations are also
sketched in Figure 6.3.
Figure 6.3:
The truncation
of the Fourier expansion of the EM field has two major impacts, namely
a low-pass filtering of the field as well as of the geometry. Hence,
also for the permittivity and its reciprocal only a certain number of
Fourier coefficients is required.
|
|
The rank of the ODE system (6.21) is now finite and
equals
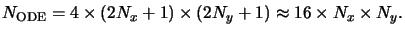 |
(6.21) |
The factor four is due to the four lateral field components, the cut-off
frequencies are counted twice to account for ``positive'' as well as
``negative'' harmonics, and the additive one results from the zeroth-order
harmonic.




Next: 6.2.6 Vector-Matrix Notation
Up: 6.2 Lateral Discretization of
Previous: 6.2.4 Scaling of the
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17