2.3.2 Grid Generation

The simplest grid type is a tensor-product grid which consists of three one-dimensional grids. All grid elements are boxes. The advantages of this kind of grid are the simple implementation of grid generators and efficient data-management and algorithms. In the past, many simulators have been equipped with a built-in grid generation tool. Orthogonal grids enabled to refine grids easily. The disadvantages are that arbitrary shaped geometries and directions cannot be resolved and the large amount of grid points appearing (see Section 2.2.3). Simulators using tensor-product grids are CADDETH [46], MINIMOS [37], or SITAR [8].

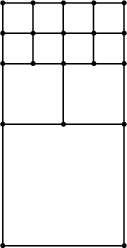
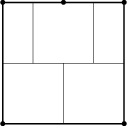
The next step is to apply a terminating line algorithm to prevent lines from going far into regions where they are not needed. In [56] a terminating line tensor-product grid is shown for the application of a thermal simulation tool. An example of such a grid is shown for the two-dimensional case in Fig. 2.13(a). Lines may be terminated to create larger grid elements. Such a grid element is depicted in Fig. 2.13(b), which is a box containing an additional point on one edge. The resulting Voronoi boxes are shown in Fig. 2.13(c). The advantage of this approach is the simple realization. The disadvantages are that a discretization error emerges due to the lack of diagonal grid lines.

(a)  Ortho-product grid with terminating lines.

(b)  Additional point on the upper edge.

(c)  Resulting boxes.

Figure 2.13: Quadtree-based grids with rectangles only.

Terminating line algorithms for tensor-product grids can be realized by using quadtrees for the two-dimensional case and octrees for the three-dimensional case. Octree-based grid generators like OMEGA [48,81,82] or CAMINO [97] allow triangles and rectangles for two dimensions and tetrahedrons and cuboids for three dimensions to improve the quality of the grid.

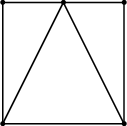
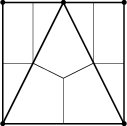
Fig. 2.14(a) shows the same box with an additional point on one edge. Triangles are used to improve the discretization. The resulting Voronoi boxes are shown in Fig. 2.14(b). Unfortunately, due to the use of different kind of grid elements, the grid generator has to be more complex.

(a)  Terminating lines with auxiliary triangulation.

(b)  Resulting boxes.

Figure 2.14: Quadtree-based grids with rectangles and triangles.

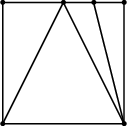
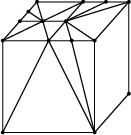
Simple gridding tools allow only one additional point in the middle of an edge. For this case, the triangulation shown before fulfills Delaunay's criterion. Obtuse angles can be avoided by restricting rectangular elements to squares. If more than one point is allowed per edge obtuse angled elements cannot be avoided as shown in Fig. 2.15 for a two-dimensional and a three-dimensional grid. Nevertheless, Delaunay's criterion is fulfilled.

(a)  Quadtree-based grid.

(b)  Octree-based grid.

Figure 2.15: Quad- and Octree-based grids allowing more than one additional point per edge.

Another kind of grid is the prismatic grid. All elements are prisms (see Fig. 2.16(d)) with a triangular base surface. In other words, instead of applying a constant thickness to rectangles which is the case in tensor-product grids, a constant thickness is applied to triangles. Therefore, the advantages are rather small: Prismatic grids enable triangulated grids in the $xy$-plane but a one-dimensional grid in the third dimension. Arbitrary shaped three-dimensional structures cannot be applied. Simulators using prismatic grids are FIELDAY [28] or SIERRA [41].

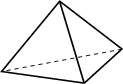
(a)  Tetrahedron.

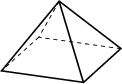
(b)  Pyramid.

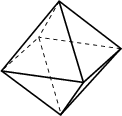
(c)  Diamond.

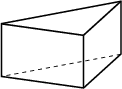
(d)  Prism.

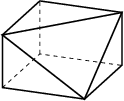
(e)  Cuboid with cut vertex.

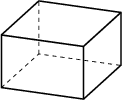
(f)  Cuboid.

Figure 2.16: Common primitives for three-dimensional grids.

Grid generators like MESH [98,99] are based on the octree method using several kinds of grid elements shown in Fig. 2.16. The use of different kinds of elements enables to achieve both a reduction of the grid density to avoid grid points in areas where they are not necessary and a reduction of the grid lines. Grids generated by MESH are used for device simulation. Nevertheless, MESH has problems with surfaces with arbitrary normal vectors.

The main disadvantage of both quadtree- and octree-based grids is that regions near arbitrary shaped surfaces cannot be described very well. The only remaining possibility for a suitable grid generator is to avoid non-Delaunay elements for hybrid grid generators or to use tetrahedras only like the grid generator DELINK [100,101,102,103].