2.4 Box Integration Method

For the discretization [73] of the differential equations the Finite-Boxes method (box integration method) is used. It uses a grid consisting of points and lines where each point ${P}_{i}$ is assigned its Voronoi box ${{\Omega}}_{i}$ (see Section 2.3.1) which is defined as its corresponding part of the simulation area. All boxes together form the whole simulation area ${\Omega}$ .

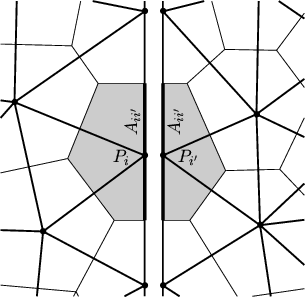
All points and therefore all the boxes are numbered. Boxes that touch each other are connected by lines. As the Voronoi diagram and the grid are dual, the inverse definition is valid too: if points are connected by lines, the corresponding boxes touch each other.

Adjacent boxes are called neighboring boxes. A box can have an arbitrary number of neighboring boxes. For the discretization an information like ``the number of the next neighboring point in order'' or ``the number of the neighbor of two neighboring points'' is not available and not needed. The discretization scheme in Minimos-NT uses unstructured neighborhood information. The advantage of this procedure is that the discretization scheme is independent of the type of the grid used. This enables to apply any kind of grid, because no special kind of grid is taken for granted. Nevertheless, the grids have to meet the criterions discussed in Section 2.3.

$\psfig{file=figures/grid/qi_4, width=7cm}$

(a) Voronoi box of an inner point.

$\psfig{file=figures/grid/qj_2, width=7cm}$

(b) Voronoi box of an interface point.

**Figure 2.17:** Neighborhood information.

The basic semiconductor equations consist of Poisson's equation, the continuity equation for electrons and holes and the equations for the current density for electrons and holes. The current relations (2.4) and (2.5) are given for the drift-diffusion case. This set of equations was first presented by Van Roosbroeck [20] in 1950.

$\displaystyle \hbox{\rm div}\,{(\varepsilon \cdot \hbox{\rm grad}\,{\psi })} = q\cdot (n- p+ {N}_{A}- {N}_{D})$

(2.1)

$\displaystyle \hbox{\rm div}\,{{\mathbf{J}}_{n}} - q\cdot \frac{{\partial}n}{{\rm d}t} = q\cdot R$

(2.2)

$\displaystyle \hbox{\rm div}\,{{\mathbf{J}}_{p}} + q\cdot \frac{{\partial}p}{{\rm d}t} = - q\cdot R$

(2.3)

$\displaystyle {\mathbf{J}}_{n}= q\cdot n\cdot {\mu }_{n}\cdot \mathbf{E}+ q\cdot {D}_{n}\cdot \hbox{\rm grad}\,n$

(2.4)

$\displaystyle {\mathbf{J}}_{p}= q\cdot p\cdot {\mu }_{p}\cdot \mathbf{E}- q\cdot {D}_{p}\cdot \hbox{\rm grad}\,p$

(2.5)

Equation (2.1) is derived from the third Maxwell equation for the dielectric displacement under assumption of a static magnetic and electric field. The equations (2.2) and (2.3) are derived from the first and the third Maxwell equations. The assumption made is that only the mobile charge represented by electrons and holes are time variant. By introducing a generation/recombination term the equations can be separated into to parts, one for electrons and one for holes as shown above. By superpositioning the current given by Ohm's law and the particle flux density for each carrier type the drift-diffusion current relations for electrons (2.4) and holes (2.5) are derived [19,73,88].

To discretize Poisson's equation (2.1) the third Maxwell equation is used. For the equations (2.1), (2.2), and (2.3) Gaussian's law is applied by integrating the equations over a Voronoi box ${{\Omega}}_{i}$ of a point ${P}_{i}$ . By approximizing the integrals with sums over all neighboring points ${P}_{j}$ the following equations are obtained:

$\displaystyle \sum_{j}{D}_{{i}{j}}\cdot {A}_{{i}{j}}= {\rho }_{i}\cdot {V}_{i},$

(2.6)

$\displaystyle \sum_{j}{{\mathbf{J}}_{n,ij}} \cdot {A}_{{i}{j}}= q\cdot \left({{R}_{i}+ \frac{{\rm d}{n}_{i}}{{\rm d}t}}\right) \cdot {V}_{i}$

(2.7)

$\displaystyle \sum_{j}{{\mathbf{J}}_{p,ij}} \cdot {A}_{{i}{j}}= - q\cdot \left({{R}_{i}+ \frac{{\rm d}{p}_{i}}{{\rm d}t}}\right) \cdot {V}_{i}$

(2.8)

${V}_{i}$ is the volume of the Voronoi box ${{\Omega}}_{i}$ and ${A}_{{i}{j}}$ is the interface area between the two adjacent Voronoi boxes ${{\Omega}}_{i}$ and ${{\Omega}}_{j}$ . ${D}_{{i}{j}}$ , ${\mathbf{J}}_{n,ij}$ , and ${\mathbf{J}}_{p,ij}$ are the projections of $\mathbf{D}$ , ${\mathbf{J}}_{n}$ , and ${\mathbf{J}}_{p}$ on the grid line between ${P}_{i}$ and ${P}_{j}$ in the middle of the line. Now, only a suitable discretization of these quantities has to be found.

An approximation of ${D}_{{i}{j}}$ can be found where ${d}_{{i}{j}}$ denotes the distance between the two neighboring points ${P}_{i}$ and ${P}_{j}$ :

$\displaystyle {D}_{{i}{j}}= - \frac{{\varepsilon }_{i}+ {\varepsilon }_{j}}{2} \cdot \frac{{\psi }_{j}- {\psi }_{i}}{{d}_{{i}{j}}}$

(2.9)

Great care has to be taken for the discretization of ${\mathbf{J}}_{n}$ and ${\mathbf{J}}_{p}$ given by (2.4) and (2.5). This is because the quantities

and

change exponentially between two grid points. Using a discretization scheme in analogy to (2.9) would require an extremely dense mesh. The method of Scharfetter-Gummel [104] has been proven to be a useful discretization of the current density. Solving the equations [88] then leads to

$\displaystyle {\mathbf{J}}_{n,ij}= \frac{q\cdot {\mu }_{n}\cdot U_{T}}{{d}_{{i}... ...a_{ij}}\right) - {n}_{i}\cdot \mathcal{B}\!\left({- \Delta_{ij}}\right)}\right)$

(2.10)

$\displaystyle {\mathbf{J}}_{p,ij}= \frac{- q\cdot {\mu }_{p}\cdot U_{T}}{{d}_{{... ...lta_{ij}}\right) - {p}_{i}\cdot \mathcal{B}\!\left({\Delta_{ij}}\right)}\right)$

(2.11)

$\displaystyle \Delta_{ij}= \frac{{\psi }_{j}- {\psi }_{i}}{U_{T}}$

(2.12)

$\displaystyle \mathcal{B}\!\left({x}\right) = \frac{x}{{\rm e}^{x} - 1} .$

(2.13)

Both the drift diffusion model and the hydrodynamic model can be obtained from the Boltzmann equation

$\displaystyle {\partial}_{t}f + \mathbf{u}\cdot \ensuremath{\ensuremath{\mathbf... ...math{\ensuremath{\mathbf{\nabla}_{\negmedspace p}} \, f}= \mathcal{Q}(f) \qquad$

(2.14)

where $s_\nu$ is

for electrons and

for holes. $\mathbf{E}$ is the electric field, $\mathbf{u}$ is the group velocity and $\mathcal{Q}$ the collision operator. A more general way is given by the solution using

moments instead of up to

for the drift diffusion model or

for the hydrodynamic model [105]. Thereby the physically motivated weight functions

$\displaystyle \phi_0$	$\displaystyle = 1$		$\displaystyle \qquad \mathbf{\phi}_1$	$\displaystyle = \mathbf{p}$	$\displaystyle = \hbar \, \mathbf{k}$
$\displaystyle \phi_2$	$\displaystyle = \mathcal{E}$	$\displaystyle = \frac{\hbar^2 \, k^2}{2 \, m}$	$\displaystyle \qquad \mathbf{\phi}_3$	$\displaystyle = \mathbf{u}\, \mathcal{E}$
$\displaystyle \phi_4$	$\displaystyle = \mathcal{E}^2$		$\displaystyle \qquad \mathbf{\phi}_5$	$\displaystyle = \mathbf{u}\, \mathcal{E}^2$
$\displaystyle \phi_6$	$\displaystyle = \mathcal{E}^3$

$\displaystyle \ensuremath{\widetilde{M}}_j = \ensuremath{\langle {\phi}_j \rangle}= \int {\phi}_j \, f \,\, \mathrm{d}^3 k.$

(2.15)

$\displaystyle {\phi_6}: \ensuremath{\langle \mathcal{E}_3 \rangle}= \frac{7 \cdot 5 \cdot 3}{8} \, k_B^3 \, \nu \, M_6$

(2.16)

is used where $\nu$ is the carrier concentration (

) with $nu = \ensuremath{\langle 1 \rangle}$ and

denotes a moment which has to be modeled properly to obtain the following set of equations [105]:

$\displaystyle \mathbf{J}_\nu$	$\displaystyle = s_\nu \, \mu_\nu \, k_B \, \Bigl( \ensuremath{\ensuremath{\mathbf{\nabla}}\, (\nu \, T_\nu)}- s_\nu \, \frac{q}{k_B} \, \mathbf{E}\, \nu \Bigr)$	(2.17)
$\displaystyle \ensuremath{\ensuremath{\mathbf{\nabla}}\cdot \mathbf{J}_\nu}$	$\displaystyle = - s_\nu \, q \, ({\partial}_{t}\nu + R_\nu)$	(2.18)

$\displaystyle \mathbf{S}_\nu$	$\displaystyle = - \frac{5}{2} \, \frac{k_B^2}{q} \, \frac{\tau_S}{\tau_m} \, \m... ...\nu \, \Theta_\nu)}- s_\nu \, \frac{q}{k_B} \, \mathbf{E}\, \nu \, T_\nu \Bigr)$	(2.19)
$\displaystyle \ensuremath{\ensuremath{\mathbf{\nabla}}\cdot \mathbf{S}_\nu}$	$\displaystyle = - \frac{3}{2} \, k_B \, {\partial}_{t}(\nu \, T_\nu) + \mathbf{... ...{2} \, k_B \, \nu \, \frac{T_\nu - T_L}{\tau_\mathcal{E}} + G_{\mathcal{E}_\nu}$	(2.20)

$\displaystyle \mathbf{K}_\nu$	$\displaystyle = - \frac{35}{4} \, \frac{k_B^3}{q} \, \frac{\tau_K}{\tau_m} \, \... ...M_6)}- s_\nu \, \frac{q}{k_B} \, \mathbf{E}\, \nu \, T_\nu \, \Theta_\nu \Bigr)$	(2.21)
$\displaystyle \ensuremath{\ensuremath{\mathbf{\nabla}}\cdot \mathbf{K}_\nu}$	$\displaystyle = - \frac{15}{4} \, k_B^2 \, {\partial}_{t}(\nu \, T_\nu \, \Thet... ...\, \nu \, \frac{T_\nu \, \Theta_\nu - T_L^2}{\tau_\Theta} + G_{\Theta_\nu} \, .$	(2.22)

For the discretization of the fluxes $\mathbf{J}_\nu$ , $\mathbf{S}_\nu$ , and $\mathbf{K}_\nu$ the projected flux between two grid points is assumed constant and the temperature for each flux

is interpolated linearly. The Scharfetter-Gummel type discretization for each flux

then gives

$\displaystyle F_{i, \, j} = - \frac{C_F}{\Delta{}x} \, \frac{\Delta{}T_F}{\ln(T... ...hcal{B}\!\left({Y_F}\right) - \xi_i \, \mathcal{B}\!\left({- Y_F}\right) \Bigr)$

(2.23)

$\displaystyle Y_F = - \frac{\ln(T_{F \, j} / T_{F \, i})}{\Delta{}T_F} \, \Bigl( s_n \, \frac{q}{k_B} \, \Delta{}\psi + \Delta{}T_F \Bigr) \, .$

(2.24)

For the discretization the inner products $\mathbf{E}\cdot \mathbf{F}$ of the fluxes are written as

$\displaystyle \mathbf{E}\cdot \mathbf{F} = - \, (\psi - {\psi }_{i}) \, \ensuremath{\ensuremath{\mathbf{\nabla}}\cdot \mathbf{F}}$

(2.25)

It is important to note, that the whole discretization is independent from the dimensionality of the device. Only the neighborhood information is needed which has been depicted at the beginning of this section. As Minimos-NT has been expanded to a three-dimensional simulator this discretization scheme did not change. Only the vectors had to support three-dimensional coordinates. In the discretization scheme above only the drift-diffusion case is shown. The hydrodynamic case, the discretization of energy-balance and other equations is shown in [73,88,106] in detail.

Vector quantities are only needed in some models. In the discretization shown above the vector quantities have been projected on the grid line between ${P}_{i}$ and ${P}_{j}$ . Therefore only the projected component of the vector contributes to the equations. It is not possible to calculate the full vector because the vector component orthogonal to the grid line is not known.

To fully determine a vector quantity on an arbitrary point in the simulation domain it is, therefore, necessary to analyze the vectors in all neighboring points. Moreover, a calculation scheme is necessary, which deals with unstructured neighborhood information only. Thus, the scheme shown in [73] has been extended to

$\displaystyle {\mathbf{V}}_{i}= {\mathbf{M}}_{i}^{-1} \cdot \sum_{j}\frac{{A}_{... ...{\mathbf{V}}_{{i}{j}} \right)} {\left\vert{\mathbf{X}}_{{i}{j}}\right\vert^2} ,$

(2.26)

$\displaystyle {\mathbf{M}}_{i}= \sum_{j}\frac{{A}_{{i}{j}}} {{d}_{{i}{j}}} \cdo... ...\mathbf{X}}_{{i}{j}}}^T \right)} {\left\vert{\mathbf{X}}_{{i}{j}}\right\vert^2}$

(2.27)

$\displaystyle {\mathbf{X}}_{{i}{j}}= \overrightarrow{{P}_{i}{P}_{j}} = \left( \... ...c} {x}_{j}- {x}_{i}\\ {y}_{j}- {y}_{i}\\ {z}_{j}- {z}_{i} \end{array} \right) ,$

(2.28)

where ${\mathbf{V}}_{i}$ denotes a vector quantity at the point ${P}_{i}$ and ${\mathbf{V}}_{{i}{j}}$ the vector quantity at the middle of the grid line between ${P}_{i}$ and ${P}_{j}$ . ${\mathbf{M}}_{i}$ is a matrix containing the weight of the neighboring points.

Since most of the equations and models contain vectors it has to be guaranteed that the formulas work for the one-, two, and three-dimensional case. Different implementations for different dimensionalities are not convenient and are a source of errors. Therefore, the quantities, the equations, and the representation of the device have to be implemented in a self-consistent way.