4.2 Die Gleichung der Besetzungsfunktion  

In diesem Abschnitt werden aus den formulierten Gleichungen der dynamischen Rekombinationsgleichung (4.5) jene diskretisierten Funktionen angegeben, die in MINIMOS-NT implementiert sind. Die Lösungsvariable, nach der gelöst wird, ist dabei die Besetzungsfunktion f_o. Die transiente Gleichung der Besetzungsfunktion f_o lautet

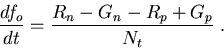$$\begin{eqnarray} \frac{d f_o}{dt}=\frac{R_n-G_n -R_p+G_p}{N_t}\; . \end{eqnarray}$$ (4.11)

Da im Bauteilsimulator die Ladungsträger getrennt behandelt werden, ist die Separation der Gleichungen entsprechend der Ladungsträgertypen notwendig. Die linke Seite von (4.11), die den transienten Anteil darstellt, kann jedoch nicht separiert werden. Der diskretisierte, mit dem Boxvolumen multiplizierte, additive Term, der im Fall der transienten Simulation in das Gleichungssystem eingetragen wird, lautet

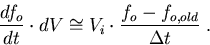$$\begin{eqnarray} \frac{d f_o}{dt}\cdot dV\cong V_i\cdot \frac{f_o-f_{o,old}}{\Delta t}\; . \end{eqnarray}$$ (4.12)

Den Anteil von (4.11), der die Elektronen betrifft, kann man mit (4.10) umschreiben zu

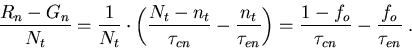$$\begin{eqnarray} \frac{R_n-G_n}{N_t}=\frac{1}{N_t}\cdot\left(\frac{N_t-n_t}{\tau... ...au_{en}}\right)=\frac{1-f_o}{\tau_{cn}}-\frac{f_o}{\tau_{en}}\; . \end{eqnarray}$$ (4.13)

Die rechte Seite von (4.13), multipliziert mit dem Volumen, wird zur diskretisierten Gleichung der Box i unter Verwendung von (4.8),(4.9)

$$\begin{eqnarray} \left(\frac{1-f_o}{\tau_{cn}}-\frac{f_o}{\tau_{en}}\right)dV\co... ...v_{th,n}\cdot\left[n-f_o\cdot \left(n+N_{n,eff}\right)\right]\; , \end{eqnarray}$$ (4.14)

mit der Abkürzung

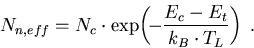$$\begin{eqnarray} N_{n,eff}= N_c\cdot\exp\!\left(\!-\frac{E_c-E_t}{k_B\cdot T_L}\right)\; . \end{eqnarray}$$ (4.15)

Der Anteil von (4.11), der die Löcher betrifft, lautet mit (4.10)

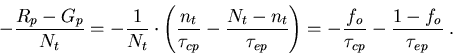$$\begin{eqnarray} -\frac{R_p-G_p}{N_t}=-\frac{1}{N_t}\cdot\left(\frac{n_t}{\tau_{... ..._{ep}}\right)= -\frac{f_o}{\tau_{cp}}-\frac{1-f_o}{\tau_{ep}}\; . \end{eqnarray}$$ (4.16)

Die mit dem Boxvolumen diskretisierte rechte Seite von (4.16) wird mit (4.8),(4.9) zu

$$\begin{eqnarray} -\left(\frac{f_o}{\tau_{cp}}-\frac{1-f_o}{\tau_{ep}}\right)dV\c... ...th,n}\cdot\left[f_o\cdot\left(p+N_{p,eff}\right)-N_{p,eff}\right] \end{eqnarray}$$ (4.17)

mit der Abkürzung

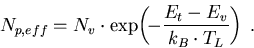$$\begin{eqnarray} N_{p,eff}= N_v\cdot\exp\!\left(\!-\frac{E_t-E_v}{k_B\cdot T_L}\right)\; . \end{eqnarray}$$ (4.18)

Die Gleichungen (4.12),(4.14),(4.17) bilden die additiven Terme der dynamischen Fehlstellengleichung. In MINIMOS-NT tragen diese Funktionen gleichzeitig die Nettorekombinationsraten in die Kontinuitätsgleichungen (4.3) und (4.4) ein. Eine weitere Funktion berechnet die zusätzliche Quellfunktion für die Poissongleichung (letzter Summand von (4.1)). Um konsistent mit dem statischen Fehlstellenmodell zu sein, wird in den Gleichungen (4.14) und (4.17)

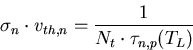$$\begin{eqnarray} \sigma_n\cdot v_{th,n}=\frac{1}{N_t\cdot \tau_{n,p}(T_L)} \end{eqnarray}$$ (4.19)

gesetzt.