9.4 The Negative Sign Problem

In the previous section we derived a stochastic interpretation of the potential scattering operator. However, the stochastic process is not of the same simple type as the classical Boltzmann scattering operator but belongs to the more general class of annihilation/creation processes [Nag00].

Consequently the Monte Carlo algorithm looses its good numerical properties. In practice simulation costs are very high and scale badly. Similar effects are observed in quantum Monte Carlo (QMC) algorithms from other fields [SK84].

The reason can be traced back to the indefinite measure represented by $V_{\mathrm{w}}$ [KG94]. In Monte Carlo theory such a property of a stochastic algorithm is termed ``the negative sign problem''.

In the special case of resonant tunneling it has the following characteristics: A unique function

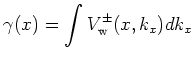
$\displaystyle \gamma(x)=\int V_{\mathrm{w}}^\pm(x,k_x)dk_x$

We interpret $\gamma$ as the out-scattering rate of the Wigner potential in strict analogy with the phonon out-scattering rate $\lambda$ , given by Equation 9.2. Stochastically the potential operator can be also interpreted as a generation term, which makes $\gamma$ a pair (particle + antiparticle) generation rate. Typically this Wigner generation rate is on the order of $10^{15} \mathrm{s}^{-1}$ . A high $\gamma$ indicates that quantum interference effects are dominant and a full quantum description is necessary. This is depicted in Figure 9.1.

**Figure 9.1:** Pair generation rate $\gamma (x)$ caused by the Wigner potential for two different voltages
$\includegraphics[width=0.9\columnwidth ]{Figures/3}$

A direct application of the QMC algorithm gives rise to an expensive computational problem. The problem is inherent to the method and can be explained as follows. For simplicity we consider the coherent case. Each trajectory starts from the boundary with unit weight which is multiplied by $\pm3$ with each scattering event, as we have the original particle plus a generated particle-antiparticle pair. This process is depicted in Figure 9.2.

**Figure 9.2:** The trajectory split algorithm: At each scattering event the weight of the trajectory is multiplied by 3 and a particle-antiparticle pair is generated.
$\includegraphics[width=0.8\columnwidth ]{Figures/mixi}$

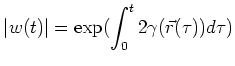$\displaystyle \vert w(t)\vert = \exp({\int_0^t 2 \gamma(\vec{r}(\tau))d\tau})$

(9.5)

For the NANOTCAD project a double barrier structure with a

nm well and

nm barriers of

eV height had to be simulated. The relevant quantum domain which surrounds the structure is approximately

nm. It can be shown that the variance of the method increases exponentially with the increase of the barrier energy and the size of the simulated domain. It is possible to use classical simulation for the electrodes combined with full quantum simulation for the barrier/well domain.

The simulated trajectories easily accumulate absolute weights of the order of magnitude of $\pm 10^{40}$ . The negative and positive weights are summed in the estimators for the physical quantities and have to cancel exactly to give a result on the order of one.

Computational cost constraints prohibit the naive application of the method for devices, where the mean accumulated weight per trajectory is larger than of the order of $\pm10^{10}$ . Only through development of variance reduction methods [KNS03] the simulation of such devices becomes possible.

In the system of Equations 9.4 potential scattering creates quasiparticles, but there is no process which annihilates quasiparticles. Hence the number of quasiparticles is not conserved but grows at an exponential rate. Consequently the variance grows exponentially with simulated time which is the manifestation of the negative sign problem. However, it is possible to introduce an annihilation process which allows for stationary solutions of the system. As long as the resulting process allows for a real stochastic interpretation (and simulation), this process may be chosen arbitrarily. The simplest choice is to add a reaction-annihilation term of the form

to the right hand side of the equations 9.4, where positive

denotes the reaction rate, which can be assumed very high. The intended interpretation is that an antiparticle and a particle which come into contact annihilate (chemically: become inert) immediately. Such processes are for instance considered in [BAR86], [KR85], [Spo88]. With the introduction of this annihilation process variance reduction is achieved and enables the simulation of realistic devices.

Finally, we observe that boundary conditions are only posed for

. Depending on the details of the Monte Carlo algorithm several choices for

and

are best suited. This is discussed in unpublished work of our colleagues Hans Kosina and Michail Nedjalkov and we cannot give any further details here.