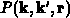Blochwellen breiten sich in einem periodischen Gitterpotential
völlig ungestört aus. Abweichungen von der idealen Periodizität, verursacht
durch thermische Gitterschwingungen, ionisierte Störstellen und
andere Kristalldefekte, führen zum Auftreten von Streuzuständen, die im
Rahmen der quantenmechanischen Störungstheorie behandelt werden können.
Zustandsänderungen werden mit Hilfe der Übergangsrate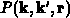 
beschrieben, die durch die goldene Regel von Fermi [32]
gegeben ist,
Der Ausgangszustand wird durch den Wellenvektor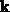 
beschrieben und besitzt
die Energie 
, der Endzustand durch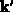 
bzw.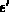 
. Der
Energiebetrag
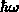tritt auf, wenn das Streupotential zeitabhängig ist
und mit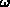 
oszilliert.
Damit man dem Zustand nach der Streuung eine scharfe Energie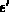
zuordnen kann,
muß die Zeit nach dem Streuvorgang gegen unendlich gehen. Für sehr häufig
aufeinanderfolgende Streuvorgänge ist diese Bedingung nicht mehr erfüllt.
In diese Fall gilt auch die strenge Energieerhaltung nicht mehr, wie
wie sie in der Gleichung 2.47 durch die Deltafunktion
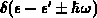repräsentiert wird.
Vielmehr tritt eine Unbestimmtheit in der Energie 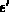auf,
ein Effekt, der als ,,collision broadening`` bezeichnet wird.
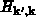ist das Matrixelement des Streupotentials zwischen den
Zuständen 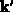und 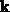, das definiert ist als
Setzt man die Wellenfunktionen 2.3 des ungestörten Problems ein, so läßt sich das Matrixelement 2.48 wie folgt faktorisieren
Das darin auftretende Kristallvolumen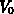 
rührt von der
Normierung der Blochfunktionen (Gleichung 2.3) her. Weiters bedeuten
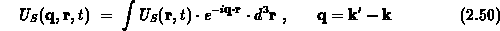
die Fouriertransformierte des Streupotentials und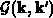 
das Überlappungsintegral
Im Überlappungsintegral gehen die gitterperiodischen Blochfaktoren ein.
Für parabolische Bänder ist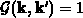 
.
Da das Überlappungsintegral für allgemeine Bänder schwierig auszuwerten ist,
ist es eine weit verbreitete Näherung, dieses im Matrixelement 2.49
eins
zu setzen. Der Einfluß des Überlappungsintegrals wird dann näherungsweise
über die Kopplungskonstante im Streupotential berücksichtigt, da diese
Kopplungskonstante in der Regel nicht genau bekannt ist und daher als
Anpassungsparameter verwendet werden kann.
Um die totale Streurate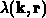 
zu erhalten,
muß über alle möglichen (diskreten)
Endzustände 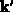summiert werden,
Die Streuraten, die wir betrachten, ändern den Spin eines Elektrons nicht.
Der symbolische Summationsindex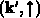 
in dieser Gleichung soll
andeuten, daß die Summation über jene Zustände 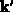erfolgt, die den
gleichen Spinzustand wie der Ausgangszustand 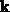besitzen.
Wenn ein Elektron im Kristallvolumen 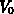lokalisiert ist, ist auch sein
Wellenvektor 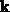quantisiert. Die Anzahl der möglichen 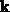-Zustände
kann entweder aus den Randbedingungen für die Schrödingergleichung oder direkt aus der
Heisenbergschen Unschärferelation bestimmt werden. Als Ergebnis kann man
sich den 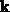-Raum in Zellen eingeteilt denken, die das Volumen
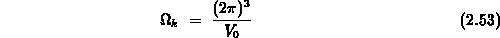
besitzen. Jede Zelle kann nun durch zwei Elektronen, die sich nur in ihrem
Spin unterscheiden, besetzt werden. Daher ist die Dichte der Zustände im
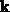-Raum gegeben durch
Mit Hilfe dieser Dichte kann man von einer Summation über diskrete Zustände zu einer Integration über kontinuierliche Zustände übergehen,
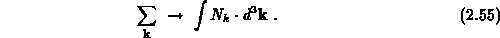
Als Integrationsbereich ist das Innere der ersten Brillouinzone zu wählen.
Bei einfacheren Bandmodellen, in denen der Rand einer Brillouinzone gar nicht
vorkommt und damit eine Beschränkung des Wellenvektors nicht auftritt, ist über den
unbeschränkten 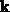-Raum zu integrieren.
In der Summation für die totale Streurate 2.52 kommen nur Zustände eines Spins in Frage, weshalb beim Übergang zur Integration die Zustandsdichte
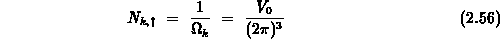
verwendet werden muß. Somit läßt sich die totale Streurate
anschreiben als
Vergleicht man diese Gleichung mit der Definition 2.37, so erhält man für die Streurate
