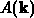 die Impulskomponente
die Impulskomponente
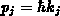 ein und gelangt so zur Impulserhaltungsgleichung in der
allgemeinen Form,
ein und gelangt so zur Impulserhaltungsgleichung in der
allgemeinen Form,




Zur Bestimmung dieser verallgemeinerten Drift-Diffusionsgleichung und der darin vorkommenden
Koeffizienten wird in [4] von der Boltzmanngleichung und der daraus unmittelbar
ableitbaren Impulserhaltungsgleichung ausgegangen.
Analog zu Abschnitt
4.2.1 setzt man in die
verallgemeinerte Bilanzgleichung 4.13
für die Observable 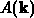 die Impulskomponente
die Impulskomponente
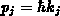 ein und gelangt so zur Impulserhaltungsgleichung in der
allgemeinen Form,
ein und gelangt so zur Impulserhaltungsgleichung in der
allgemeinen Form,
Der Term in großen Klammern auf der linken Seite kann als äußere treibende Kraft interpretiert werden, die die Drift der Elektronen verursacht. Der rechte Term beschreibt die örtliche Impulsabgaberate der Elektronen an das Gitter, die durch die Streuprozesse bestimmt wird. Motiviert durch die linke Seite dieser Gleichung kann man nun folgende Stromgleichung ansetzen,
Der formale Unterschied zu der erweiterten Drift-Diffusionsstromgleichung
4.28 besteht lediglich
darin, daß wir aus
Gründen der Allgemeinheit noch die Tensoreigenschaften der Koeffizienten
mitführen.
Die Koeffizienten in dieser Gleichung hängen von der Verteilungsfunktion ab, sie sind
also Funktionale von 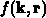 und können nun in den kritischen Bereichen
eines Bauelementes, wo starke Feldgradienten vorherrschen, mit Hilfe der Monte-Carlo-Methode
berechnet werden. Zu diesem Zweck wird in der Originalarbeit [4]
vorgeschlagen, die ersten drei Momente auszuwerten :
und können nun in den kritischen Bereichen
eines Bauelementes, wo starke Feldgradienten vorherrschen, mit Hilfe der Monte-Carlo-Methode
berechnet werden. Zu diesem Zweck wird in der Originalarbeit [4]
vorgeschlagen, die ersten drei Momente auszuwerten :

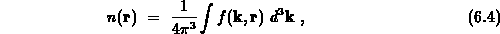

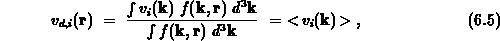

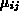 und
und
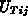 können dann einfach durch Einsetzen dieser Mittelwerte in die
Impulserhaltungsgleichung 6.2 und anschließenden Vergleich
mit den Stromgleichungen 6.1 und 6.3 ermittelt werden,
können dann einfach durch Einsetzen dieser Mittelwerte in die
Impulserhaltungsgleichung 6.2 und anschließenden Vergleich
mit den Stromgleichungen 6.1 und 6.3 ermittelt werden,
Die Idee ist also, die Monte-Carlo-Ergebnisse 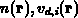 und
und
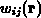 in
die Drift-Diffusionskoeffizienten
in
die Drift-Diffusionskoeffizienten 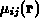 und
und 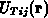 umzurechnen,
um mit
diesen Koeffizienten das Bindeglied zwischen dem Monte-Carlo- und dem Drift-Diffusionsmodell zu
erhalten. Die Stromgleichung 6.3 kann nun für die Bauelementsimulation
verwendet werden, wobei nun
umzurechnen,
um mit
diesen Koeffizienten das Bindeglied zwischen dem Monte-Carlo- und dem Drift-Diffusionsmodell zu
erhalten. Die Stromgleichung 6.3 kann nun für die Bauelementsimulation
verwendet werden, wobei nun
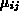 und
und 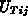 aus einer Monte-Carlo-Rechnung stammen.
aus einer Monte-Carlo-Rechnung stammen.
Diese Art der Herleitung der Koeffizienten für die Transportgleichung aus den ersten drei Momenten beweist die Allgemeingültigkeit dieser Methode. So gehen die Modelle für die Streuraten und die Bandstruktur, in welcher Komplexität sie auch immer gehalten sein mögen, über die Verteilungsfunktion direkt in die Momente und damit in die Transportkoeffizienten ein.
Die Koeffizienten 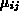 und
und 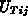 haben im Nichtgleichgewichtsfall
keine unmittelbare physikalische Bedeutung. Sie sind lediglich so definiert,
daß die Stromgleichung 6.3 die Monte-Carlo-Ergebnisse reproduziert.
In [4] wird darauf hingewiesen, daß auch andere Stromgleichungen
denkbar wären. Für diese ließen sich ebenfalls Kopplungskoeffizienten
derart definieren, daß die Monte-Carlo-Ergebnisse exakt reproduziert werden.
Die Stromgleichung 6.3 ist jedoch dadurch ausgezeichnet,
daß sie bei
Annäherung an das thermodynamische Gleichgewicht in die klassische Drift-Diffusionsstromgleichung übergeht.
In diesem Limes bekommen die Koeffizienten
haben im Nichtgleichgewichtsfall
keine unmittelbare physikalische Bedeutung. Sie sind lediglich so definiert,
daß die Stromgleichung 6.3 die Monte-Carlo-Ergebnisse reproduziert.
In [4] wird darauf hingewiesen, daß auch andere Stromgleichungen
denkbar wären. Für diese ließen sich ebenfalls Kopplungskoeffizienten
derart definieren, daß die Monte-Carlo-Ergebnisse exakt reproduziert werden.
Die Stromgleichung 6.3 ist jedoch dadurch ausgezeichnet,
daß sie bei
Annäherung an das thermodynamische Gleichgewicht in die klassische Drift-Diffusionsstromgleichung übergeht.
In diesem Limes bekommen die Koeffizienten
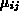 und
und
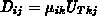 die
Bedeutung einer physikalischen Beweglichkeit beziehungsweise eines
physikalischen Diffusionskoeffizienten.
die
Bedeutung einer physikalischen Beweglichkeit beziehungsweise eines
physikalischen Diffusionskoeffizienten.
Die allgemeine Stromgleichung 6.3 gibt daher sowohl den Nichtgleichgewichtsfall wieder, indem sie einfach die Monte-Carlo-Ergebnisse nachbildet, als auch den Gleichgewichtsfall, welchen sie mit der ohmschen Beweglichkeit
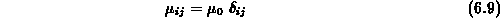
und der Temperaturspannung im Gleichgewicht
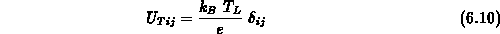
von sich aus wiedergibt.
Aus diesen Betrachtungen wird ein weiterer Vorteil dieses hybriden Modells
erkennbar. Nachdem sowohl die Hoch- als auch die Niederfeldgebiete eines
Bauelementes mit ein und derselben Stromgleichung behandelt werden, tritt für die
in dieser Gleichung vorkommenden Größen 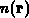 und
und 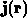 , also für
die ersten beiden Momente, das
Problem der Übergangsbedingungen erst gar nicht auf. Für
, also für
die ersten beiden Momente, das
Problem der Übergangsbedingungen erst gar nicht auf. Für 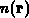 und
und
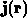 ist der stetige Übergang somit automatisch gegeben,
für die Koeffizienten
ist der stetige Übergang somit automatisch gegeben,
für die Koeffizienten 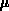 und
und 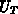 ist er auf Grund der oben diskutierten,
physikalisch sinnvollen Wahl von Gleichung 6.3 ebenfalls erfüllt.
ist er auf Grund der oben diskutierten,
physikalisch sinnvollen Wahl von Gleichung 6.3 ebenfalls erfüllt.



