 |
Der eigentliche Grund für die Notwendigkeit von Anpassungszerlegungen sind die bei der Verfeinerung generierten Punkte an der Oberfläche eines Elementes. Diese Punkte müssen nämlich auch von den angrenzenden Elementen referenziert werden, sodaß diese erst entsprechend verfeinert (angepaßt) werden. Die Verfeinerungsroutine erhält also die Menge der zusätzlich notwendigen Punkte in einem Element als Eingabe und muß eine entsprechende Zerlegung des Elementes aus den möglichen Zerlegungen auswählen.
Im Zuge des Programmablaufes muß daher die Konfiguration und die Permutation der anzuwendenden Zerlegung anhand der existierenden neuen Punkte ermittelt werden. Während im Fall des Dreiecks inklusive der vollständigen Zerlegung und aller Permutationen nur vier Zerlegungsvarianten zugelassen sind, treten beim Tetraeder und beim Oktaeder bereits wesentlich mehr Möglichkeiten auf und man benötigt daher ein effizientes Verfahren zur Ermittlung der passenden Zerlegung.
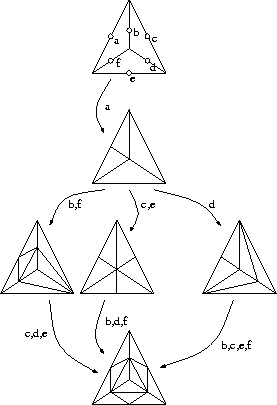
Die zur Auswahl stehenden Zerlegungen unterscheiden sich durch die dabei vorhandenen zusätzlichen Knoten. Durch Hinzufügen eines oder mehrerer Knoten erhält man die Punktkonstellation einer bestimmten Zerlegung. Beim Hinzufügen weiterer Punkte erreicht man weitere Zerlegungen, bis alle zusätzlich möglichen Punkte existieren und die vollständige Verfeinerung vorliegt. Abb. 7.8 zeigt dies anhand eines Graphen, der diesen Vorgang am Beispiel des Tetraeders beschreibt.
 |
Durch das Einfügen eines einzelnen Punktes (hier Punkt a) muß der Tetraeder in zwei Teile geteilt werden. Sollen weitere Punkte eingefügt werden, hängt der weitere Weg von den zusätzlichen Punkten ab. Will man jetzt z.B. den Punkt f hinzufügen, so kann nur dann eine Zerlegung gefunden werden, wenn auch Punkt b dazugenommen wird.
Diese Abhängigkeiten können als binärer Baum dargestellt werden, wo je nach Existenz des betreffenden Punktes verzweigt wird. Nach Überprüfung aller Punkte (beim Tetraeder a-f) enthalten die Blätter des Baumes die jeweils entsprechende Zerlegung. Stößt man auf eine Punktkonstellation, die durch keine der tabellarisch erfaßten Zerlegungen dargestellt wird, extrahiert der Algorithmus gleich eine mögliche feinere Zerlegung und die dazu nötigen zusätzlichen Punkte. In diesem Fall müssen diese zusätzlichen Punkte generiert und von den Nachbarn referenziert werden.
Zur Ermittlung einer geeigneten Anpassungszerlegung muß der Algorithmus jeden möglichen zusätzlichen Punkt im Element einmal überprüfen. Damit ist der Aufwand zur Ermittlung der entsprechenden Zerlegung proportional der zu überprüfenden Punkte innerhalb eines Elementes. Wiederum wird der binäre Suchbaum automatisch zum Zeitpunkt der Übersetzung erzeugt, sodaß der dazu nötige Aufwand die Rechenzeit nicht beeinflußt.
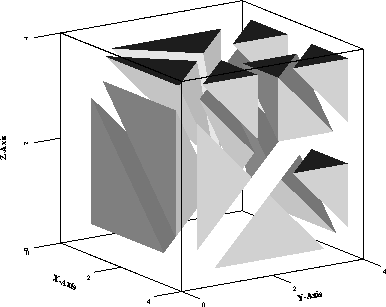
Zur Illustration des beschriebenen Verfahrens werden zwei aufeinanderfolgende Verfeinerungsschritte eines würfelförmigen Gebietes gezeigt. Abb. 7.9 zeigt das aus sechs Tetraedern bestehende Initialgitter. Die Gitterelemente wurden dabei verkleinert dargestellt, um Einblick in das Innere zu gestatten.
Im ersten Verfeinerungsschritt wird die vollständige Verfeinerung des rechten oberen Tetraeders durchgeführt. Durch die Anpassungszerlegung werden noch drei weitere Tetraeder verfeinert. Abb. 7.10 zeigt das Gitter nach dem ersten Verfeinerungsschritt.
Zur Demonstration der rekursiven Anwendung wird das vorderste Kind des bereits verfeinerten Tetraeders vollständig verfeinert. Nun pflanzt sich die Verfeinerung weiter fort (Abb. 7.11), sodaß nun auch indirekte Nachbarn des ursprünglich verfeinerten Tetraeders verfeinert werden müssen, um mit den zur Verfügung stehenden Anpassungszerlegungen die Gitterkonsistenz erfüllen zu können.
 |
 |