Das Präzipitationsverhalten der {311}-Defekte läßt sich mittels Gl. 2.16
beschreiben. Das Verhalten wird vom effektiven Reaktionskoeffizienten ![]() und den
Gleichgewichtskonzentrationen Cn* bestimmt. Diese sind durch
Gl. 2.18 von der Oberflächen- und Deformationsenergie
und den
Gleichgewichtskonzentrationen Cn* bestimmt. Diese sind durch
Gl. 2.18 von der Oberflächen- und Deformationsenergie ![]() abhängig. Sowohl in [Gen97] als auch in [Hob97] und [Dun93]
wird davon ausgegangen, daß sich sowohl die Deformationsenergie als auch die
Oberflächenenergie des planaren Defektes mit
abhängig. Sowohl in [Gen97] als auch in [Hob97] und [Dun93]
wird davon ausgegangen, daß sich sowohl die Deformationsenergie als auch die
Oberflächenenergie des planaren Defektes mit
Bei der Modellierung des effektiven Reaktionskoeffizienten ![]() muß auf das
Wachstumsverhalten der Defekte Rücksicht genommen werden. Nachdem die Defekte hauptsächlich in
der Länge wachsen, während die Breite nach oben begrenzt ist, kann man annehmen, daß die
Einbindung zusätzlicher Atome nur an den kurzen Kanten eines Rechteckes einer Breite w und
der Länge l stattfindet (siehe Abb. 3.1). Aus der Lösung des stationären lokalen
Diffusionsfeldes in der Umgebung der Reaktionszonen an beiden Enden eines Defektes läßt sich
nach [Hob97] der diffusionslimitierte Reaktionskoeffizient
muß auf das
Wachstumsverhalten der Defekte Rücksicht genommen werden. Nachdem die Defekte hauptsächlich in
der Länge wachsen, während die Breite nach oben begrenzt ist, kann man annehmen, daß die
Einbindung zusätzlicher Atome nur an den kurzen Kanten eines Rechteckes einer Breite w und
der Länge l stattfindet (siehe Abb. 3.1). Aus der Lösung des stationären lokalen
Diffusionsfeldes in der Umgebung der Reaktionszonen an beiden Enden eines Defektes läßt sich
nach [Hob97] der diffusionslimitierte Reaktionskoeffizient ![]() approximieren:
approximieren:
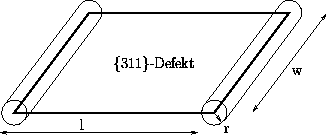 |
Die Reaktionszonen werden an den beiden Enden des Defektes als Zylinder mit der
Länge w und dem Radius r0 angenommen, welcher gleich der Gitterkonstante (5.43Å) gesetzt
wird. Bei geringer Länge l verschmelzen die beiden Zylinder zu einer gemeinsamen Hülle,
sodaß im Grenzfall l=0 nur mehr einer übrigbleibt. Dieser Tatsache wird durch den
geometrischen Faktor fg Rechnung getragen, welcher einer Interpolation zwischen
den Grenzwerten für l=0 und ![]() entspricht.
entspricht.
Der reaktionslimitierende Anteil des Reaktionskoeffizienten ergibt sich unter Verwendung von
Gl. 2.10, Gl. 2.14 und Gl. 3.7 zu
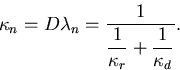 |
(3.11) |