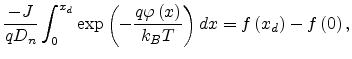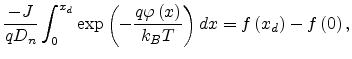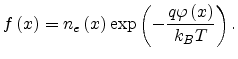


Next: 8. Conclusion
Up: 7. Organic Semiconductor Device
Previous: 7.2 Analytical Model for
Subsections
In this section we present a unified device model for unbipolar OLEDs which
includes charge injection, transport, and space charge effects in the organic
material.
In order to analyze the interplay between charge injection and bulk
conductivity one must use specific models for both injection and charge
transport in bulk. Here we treat the charge injection as diffusion
controlled and the transport within multiple trapping theory as presented in
Chapter 5. By multiplying
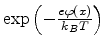 in both sides of
(5.2) and integrating
in both sides of
(5.2) and integrating 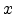 from 0 to
from 0 to 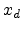 , we obtain
, we obtain
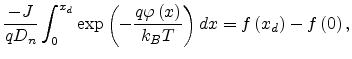 |
(7.18) |
where 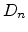 is the diffusion coefficient and
is the diffusion coefficient and
In the transport regime of the device, the potential expression (5.1) does not
hold true anymore, instead, the potential must be calculated from the Poisson equation
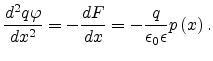 |
(7.19) |
In the bulk regime, (5.2) is rewritten as
![$\displaystyle p_e\left(x\right)=\left[p_e\left(x_d\right)-\frac{J}{qD_n}\int_0^...
...T}\right)\right] \times\exp\left(-\frac{p\varphi\left(x\right)}{k_BT}\right).$](img634.png) |
(7.20) |
In order to calculate the  characteristics of OLEDs, one must solve (7.19)
together with (5.4) and (7.20) self-consistently. The injection boundary conditions are
characteristics of OLEDs, one must solve (7.19)
together with (5.4) and (7.20) self-consistently. The injection boundary conditions are
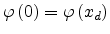 ,
,
 and
and
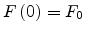 .
With the device model presented above we calculate the device characteristics
of one carrier type at different barrier height
.
With the device model presented above we calculate the device characteristics
of one carrier type at different barrier height 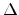 , as shown in Fig 7.9. The
input parameters are
, as shown in Fig 7.9. The
input parameters are 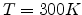 ,
,
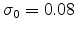 eV,
eV,
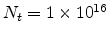 cm
cm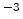 ,
,
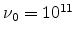 s
s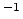 ,
,
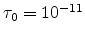 s,
s,
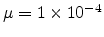 cm
cm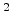 /Vs and the device length is 100
/Vs and the device length is 100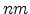 . The comparison between
our work and experimental data of hole only ITO/NPB/Al [135] is
plotted in Fig 7.10 with
. The comparison between
our work and experimental data of hole only ITO/NPB/Al [135] is
plotted in Fig 7.10 with
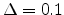 eV,
eV,
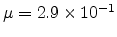 cm
cm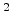 /Vs and device length 65
/Vs and device length 65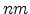 . The other
parameters are the same as in Fig 7.9. The current is neither the pure injected limited
current nor SCLC [135].
. The other
parameters are the same as in Fig 7.9. The current is neither the pure injected limited
current nor SCLC [135].
A single carrier OLED model including charge injection and transport is presented
here. This model is based on a Gaussian DOS and multiple trapping theory. It can
explain barrier height dependence of current/voltage characteristics and
agrees with experimental data [135].
Figure 7.9:
Barrier height dependence of current/voltage characteristics for
unbipolar OLED.
|
|
Figure 7.10:
Comparison between the model and experimental data for unbipolar OLED.
|
|



Next: 8. Conclusion
Up: 7. Organic Semiconductor Device
Previous: 7.2 Analytical Model for
Ling Li: Charge Transport in Organic Semiconductor Materials and Devices