Polar Optical Phonon Scattering

5.3 Polar Optical Phonon Scattering

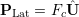
In polar semiconductors the electron-longitudinal optical (LO) phonon scattering is the dominant intersubband scattering mechanism for separations of the subbands less than the LO phonon energy [83]. Due to the polarization in polar semiconductor crystals induced by the optical vibration mode, the electrons are scattered through the interaction of the Coulomb field of the lattice polarization waves.

In optical vibrations the atoms in a lattice vibrate against each other, which can produce polarization effects. For longitudinal optical vibrations there is an restoring force due to the polarization field generated by the vibration. The lattice polarization P_Lat is proportional to the lattice displacement U and the Fröhlich constant F_c

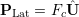ˆ PLat = FcU

(5.8)

where F_c is given by [84]

[ℏ ωLO 2 ( 1 1 ) ]1∕2 Fc = --2-- ϵ0 ε-- - ε- ∞ s

(5.9)

Here, ϵ₀ is the vacuum dielectric constant, ε_s and ε_∞ are the static dielectric permittivity and high frequency dielectric permittivity.

An electric displacement D is generated by the charge distribution according to

∇ ⋅D = ρ(x )

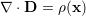(5.10)

The interaction potential ΔÛ between the external electric displacement and the lattice polarization reads

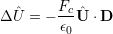ΔUˆ = - FcˆU ⋅D ϵ0

(5.11)

with

1 ∑ Uˆ = √--- q [ˆaqeiq⋅x + ˆa†qe-iq⋅x] V q

(5.12)

where â _q and â_q^† denote the annihilation and creation operators. The summation over all generated dipoles result in the total interaction Hamiltonian, hence

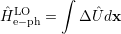∫ HˆLOe-ph = Δ ˆUdx

(5.13)

An electron located at x generates a displacement at x^′ according to

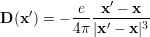e x′ - x D (x′) = ------′----3 4π |x - x|

(5.14)

which yields an interaction Hamiltonian of the form

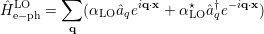LO ∑ iq⋅x ⋆ †- iq⋅x Hˆe-ph = (αLOˆaqe + αLOˆa qe ) q

(5.15)

where the coupling coefficent is given by

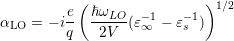( )1 ∕2 αLO = - ie ℏωLO-(ε-∞1- ε-s1) q 2V

(5.16)

The scattering rate for an electron initially in subband ν and stage λ to a final subband ν^′ and stage λ^′ , can be written as (see Appendix B.1)

( ) ( ) 1 e2ℏ-ωLOm-⋆ν′λ′- -1- 1- 1- 1- η η′ τν′λ′(k∥)= 4ℏ3 ε∞ - εs NLO + 2 ∓ 2 Θ(E νλ(k )- Eν′λ′ ± ℏωLO + Δ λλ′) νλ ∫ νλ 2 × dq -----------|F-ν′λ′(qz)|------------ (5.17) zq4z + (Q νν′λλ′)4± + 2q2z[2k2∥ ± (Q νν′λλ′)2±]

where m^⋆ is the electron effective mass, ℏω_LO is the longitudinal optical phonon energy. Here, Δ_λλ^′ denotes the energy change due to reinjection of the electron into the central region after an interstage scattering process

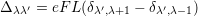Δ λλ′ = eFL (δλ′,λ+1 - δλ′,λ-1)

(5.18)

[next] [prev] [prev-tail] [front] [up]