5.4 Acoustic Deformation Potential Scattering

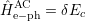
In this section, the coupling of the electrons with acoustic phonons is analyzed. Displacement of the atoms from their lattice sites are induced by crystal vibrations, which induces a modification of the bandstructure. For electrons in the conduction band, the variation of the conduction band edge E_c can be induced by acoustic phonons and the corresponding interaction Hamiltonian Ĥ_e-ph^AC is given by

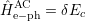(5.19)

For small displacements δE_c can be written as

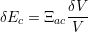(5.20)

where Ξ_ac denotes the acoustic deformation potential and δV is the variation of the crystal volume V . The local variation of the volume results from the lattice displacement U = x^′- x. The volume of a cube generated by the orthogonal vectors a = (δx,0,0), b = (0,δy,0) and c = (0,0,δz), is given by

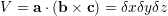(5.21)

The cube is distorted according to the transformations

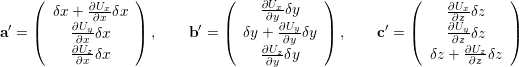
and the new volume can be written as

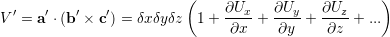(5.22)

Since

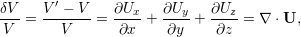(5.23)

where the lattice displacement is given by  [85]

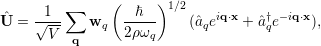(5.24)

the interaction Hamiltonian reads

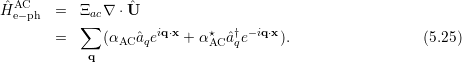
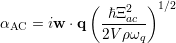(5.26)

The electron scattering rate with the assistance of acoustic phonons can be written in the following form  [87] (see Appendix B.2)

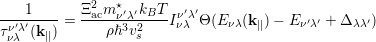(5.27)

where E_ac is the acoustic deformation potential, ρ is the density of the material, and v_s stands for the sound velocity. This equation is only valid for ℏω_q ≪ k_BT, i.e. when the thermal energy is much larger than the energy of the phonon involved in the transition, and in the elastic approximation limit ℏω_q → 0 (see Appendix B.2).