[next] [prev] [prev-tail] [tail] [up]

5.7 Interface Roughness Scattering

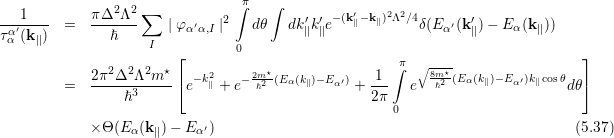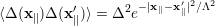
The roughness of interfaces in a heterostructure leads to spatial fluctuations of the well width, and consequently to fluctuations of the energy levels. These fluctuations of the energy levels act as a fluctuating potential for the motion of confined carriers  [89]. A distribution of terraces is present at the interfaces and the electrons are scattered elastically by them  [90].

The randomness of the interface is described by a correlation function at the in-plane position x∥= (x, y), which is usually taken to be Gaussian with a characteristic height of the roughness Δ, and a correlation length Λ representing a length scale for fluctuations of the roughness along the interface  [91], such that

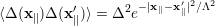′ 2 -|x∥-x′∥|2∕Λ2 ⟨Δ (x∥)Δ (x ∥)⟩ = Δ e
(5.32)

The perturbation in the potential V (z) due to a position shift Δ(x∥) is given by

dV-(z)- δV = V[z - Δ(x∥)]- V (z) ≈ - Δ (x∥) dz
(5.33)

For the I-th interface, which is centered about the plane zI and extends over the range [zL,I,zR,I], the scattering matrix element can be defined as

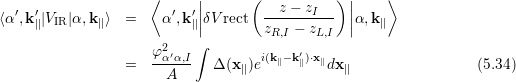
⟨ || ( z - zI ) || ⟩ ⟨α′,k′∥|VIR |α,k ∥⟩ = α ′,k′∥||δV rect ---------- ||α,k∥ ∫ zR,I - zL,I φ2α′α,I- i(k∥-k′∥)⋅x∥ = A Δ (x∥)e dx∥ (5.34)
where |α′ ⟩ and |α⟩ denote the final and initial wave functions, respectively. Here, φα′α,I is defined as
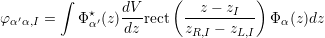∫ dV ( z - zI ) φ α′α,I = Φ⋆α′(z)---rect ---------- Φ α(z)dz dz zR,I - zL,I
(5.35)

and the rectangular function reads

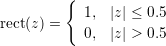
{ rect(z) = 1, |z| ≤ 0.5 0, |z| > 0.5

The expectation value of the square of the matrix element is given by

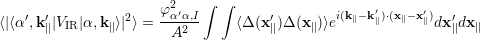′ ′ 2 φ2α′α,I∫ ∫ ′ i(k∥- k′)⋅(x∥-x′) ′ ⟨|⟨α ,k ∥|VIR|α,k∥⟩| ⟩ =--A2-- ⟨Δ(x∥)Δ (x∥)⟩e ∥ ∥ dx∥dx∥
(5.36)

Making use of eq. (5.32) and Fermi’s Golden Rule, the interface roughness induced scattering rates are given by  [92]

∫π ∫ 1 π-Δ2Λ2-∑ ′ 2 ′′ - (k′∥-k∥)2Λ2∕4 ′ ′ τα′α(k∥)= ℏ | φα α,I | dθ dk∥k∥e δ(Eα (k∥)- E α(k∥)) I ⌊ 0 ⌋ 2 2 2 ⋆ 2 2m⋆ ∫π ∘-8m-⋆ = 2π--Δ-Λ--m- ⌈e- k∥ + e--ℏ2 (Eα(k∥)-E α′) + 1- e ℏ2 (Eα (k∥)- Eα′)k∥cosθdθ⌉ ℏ3 2π 0 × Θ(E α(k∥)- E α′) (5.37)
where k ∥ ′ and k∥ are the final and initial wave vectors, respectively, and θ is the scattering angle. The integral is evaluated numerically by means of the MATLAB integration routines.

[next] [prev] [prev-tail] [front] [up]