[prev] [prev-tail] [tail] [up]

5.8 Alloy Scattering

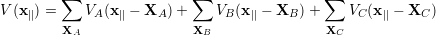
We consider an alloy AxB1-xC, where the atoms A and B are distributed randomly and the crystal potential V (x ∥ ) is not periodic. In general, the crystal potential of an alloy can be represented in terms of an average potential V (x∥), which is periodic, plus a fluctuating potential δV (x∥) which describes the local departure of the actual alloy potential V (x∥) from the average potential V (x∥). An effective scattering process (alloy scattering) is introduced by this fluctuating potential δV (x ∥ ).

Here, we will introduce the most important expressions and identities for the mentioned potentials, and the detailed derivation of the alloy scattering rate can be looked up in Appendix B.6. The crystal potential for the alloy AxB1-xC is the superposition of the potential contributed by the atoms A, B and C, which can be written as  [93]

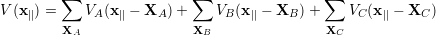∑ ∑ ∑ V(x∥) = VA (x∥ - XA ) + VB (x∥ - XB ) + VC (x∥ - XC ) XA XB XC
(5.38)

By introducing the mathematical identities

VA(x∥- XA ) = xVA(x∥ - XA )+ (1 - x)VB(x∥ - XA )+ (1 - x)VA(x∥ - XA ) - (1 - x)VB(x∥ - XA ) VB(x∥- XB ) = xVA(x∥ - XB )+ (1 - x)VB(x ∥ - XB )- xVA(x∥ - XB ) +xV (x - X ) B ∥ B
the crystal potential is given by
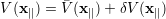V (x∥) = V¯(x∥)+ δV (x∥)
(5.39)

where the average lattice potential V (x∥) can be written as

¯V(x)= ∑ xV (x - X ) + (1 - x)V (x - X )+ ∑ V (x - X ) ∥ A ∥ i B ∥ i C ∥ C Xi={XA,XB} XC
(5.40)

and the fluctuating potential δV (x∥) reads

δV(x)=∑(1- x )[V (x - X )- V (x - X )]+ ∑ x[V (x - X ) - V (x - X )] ∥ A ∥ A B ∥ A B ∥ B A ∥ B XA XB (5.41)
The alloy scattering rate can be expressed as  [94]
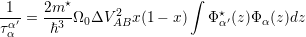⋆ ∫ -1′= 2m--Ω0ΔV A2Bx (1- x) Φ ⋆α′(z)Φα (z)dz ταα ℏ3
(5.42)

In heterostructures, the alloy scattering rate is found to be independent of the electron kinetic energy. The volume of the elementary cell is given as Ω0 = a02∕4.

[prev] [prev-tail] [front] [up]