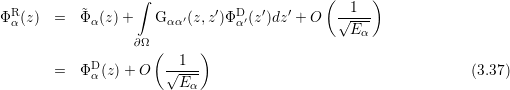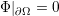
Stationary transport of charge carriers in semiconductor devices is modeled by means of boundary value problems. In order to investigate systems with net current flows and to obtain current-voltage characteristics of a quantum device, one has to impose boundary conditions which allow current carrying states 1 .
Homogeneous Neumann or Dirichlet boundary conditions yield a self-adjoint Hamiltonian matrix and cannot be used for open systems, since there is no interaction with the environment and the current density is identical zero [48]. A popular approach is to assume periodic boundary conditions which ensure the continuity of the current density, but in fact closes the system and makes the investigation of open system aspects impossible. The simulation domain is usually taken to be finite and the boundaries are physically given by electrical contacts. This leads to the necessity to consider open quantum systems with non-selfadjoint boundary conditions.
In the following chapters, the focus is on boundary conditions which yield current carrying states as solutions of the Schrödinger equation. The theoretical development is based on a Robin boundary condition approach when a solution with the Dirichlet boundary condition is available [49]. A transformation converts a wave function satisfying a Dirichlet boundary condition to a wave function satisfying a Robin boundary condition, enabling particle exchange across the boundary. We also prove that the solution of the Robin problem converges to the solution of the Dirichlet problem, as the energy tends to infinity [50].
If Ω is the domain of the device and ∂Ω denotes the corresponding boundary, it is standard to define self-adjoint realizations of the Hamiltonian by imposing Dirichlet boundary conditions
|
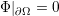| (3.17) |
or Neumann boundary conditions
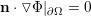 | (3.18) |
where n is the outward normal vector of the boundary. The physical meaning of the Neumann boundary condition, which fixes the normal derivative of the field at the boundary, is the constant flux in and out of the simulation domain.
Let Ω = [0, L] be the domain of the QCL perpendicular to quantum well layers. Assuming an incoming wave from -∞ with amplitude 1 and no wave incident from +∞, the Schrödinger equation can be solved explicitly outside the domain Ω
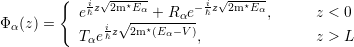
where V (z) = 0 on (-∞,0) and V (z) = V (L) = V L < 0 for z > L. We can deduce a boundary condition at ∂Ω ∈{0,L} that does not involve reflection and transmission coefficients [51]
In order to construct a solution to the Schrödinger equation with Robin boundary conditions when a solution to the same equation with Dirichlet boundary conditions is available, we make use of a Dirichlet-to-Robin transform [49]. If ΦR(z) satisfies the Robin boundary condition at ∂Ω
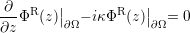 | (3.21) |
the function
 | (3.22) |
corresponds to the solution of the Dirichlet problem, ΦD(z)
∂Ω = 0. For a given function ΦD(z), the
general solution to the differential equation (3.22) can be written as
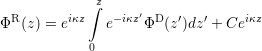 | (3.23) |
The boundary condition (3.20) gives κ =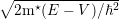 
. The constant C is evaluated by
the requirement that ΦR(z) must satisfy the boundary condition (3.19) at z = 0, which
gives
 | (3.24) |
where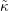 
= 
.
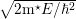Including a source term Q, we consider the most general effective mass Schrödinger equation in
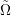:= Ω \ ∂Ω
![[ 2 ]
- ℏ--∂---1⋆---∂--+ V(z)- E α Φα(z) = Qα(z)
2 ∂z m (z) ∂z](diss_html35x.png) | (3.25) |
where Ω is the bounded domain with the boundary ∂Ω. The corresponding Green’s function is given by [52]
![2 [ ]
G αα′(z,z′) = --- Φα(z)Φ ⋆α′(z′)Θ (z - z ′)+ Φ α′(z)Φ ⋆α(z′)Θ (z′ - z)
c](diss_html36x.png) | (3.26) |
where Θ is the Heaviside function and c is a constant. Considering the Dirichlet boundary value problem
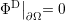 | (3.27) |
the solution for the effective mass Schrödinger equation at energy Eα ∈ ℝ can be written in terms of the Green’s function as follows
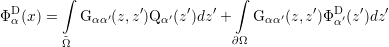 | (3.28) |
The solution of the Robin boundary value problem
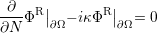 | (3.29) |
converges to ΦD as E →∞.
Proof.Let
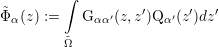 | (3.30) |
Then Φα R (z) =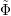 
α(z) + ΦαT(z), where ΦαT(z) satisfies
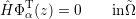 | (3.31) |
Due to the boundary condition (3.29) the following relation holds at the boundary
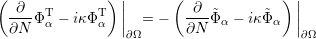 | (3.32) |
In general, Φα T can be written in the form
 | (3.33) |
where φ can be determined by inserting equation (3.33) into the condition (3.32), which yields the following equation
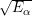), we get
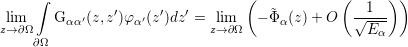 | (3.34) |
Inserting the equations (3.27) and (3.28) yields
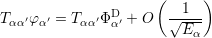 | (3.35) |
where the operator T is defined as follows
 | (3.36) |
Thus,
