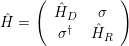
The NEGF formalism provides a generalized microscopic theory for quantum transport. It adresses the problem of dissipative transport and desribes open systems fully quantum mechanically. The theory behind it is deeply rooted in the many-body theory [53].
The information of the many-particle system is put into self energies, which are part of the equations of motion for the Green’s functions. The Green’s functions can be calculated from perturbation theory and describe the correlation between two operators at times t and t′. A detailed description and justification of the Green’s functions and self energies can be found for instance in the work of Datta [54]. Here, I will only summarize the most important definitions and provide a physical interpretaion.
The Hamiltonian of an open system coupled to a reservoir can be written as [55]
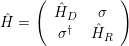
ĤDand Ĥ R denote the Hamilton operators of the device and reservoir, respectively, and σ is the coupling matrix. The corresponding Schrödinger equation of the channel-reservoir system can be expressed as [56]
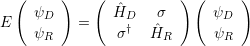
ψD and ψR denote the wave functions of the channel and the reservoir. The steady state equation for the Green’s function is defined as
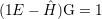 | (3.38) |
Thus, the corresponding Green’s function to the device-reservoir system can be written as

The coupling between the device and the reservoir is described by GDR and GRD. The retarded Green’s function G reads
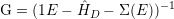 | (3.39) |
and includes the self energy which describes the interaction between the device and the reservoir [57]. The inclusion of the self energy reduces the Green’s function of the reservoir to the dimension of the Hamiltonian of the device. The self energy is determined iteratively and satisfies
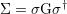 | (3.40) |
The matrix form of the density of states is the spectral function As which is given by
 | (3.41) |
The electron density is provided by the density matrix
 | (3.42) |
where fE is the Fermi-Dirac distribution function and EF denotes the Fermi energy.