The interband optical matrix element for a transition from an eigenstate in the valance subband to another eigenstate in the conduction subband is calculated in Sec. 3.1.3. These matrix elements determine the selection rules for optical transitions [166]. A zero matrix element means a forbidden transition. To determine a transition rule, it is sufficient to determine the symmetry of the transition matrix element. If the symmetry of this element spans the totally symmetric representation of the point group to which the unit cell belongs then its value is not zero and the transition is allowed. Otherwise, the transition is forbidden. Assuming a uniform potential profile across the ribbon’s width, the subband’s wave functions are either symmetric or anti-symmetric along the y-axis direction (ψc∕v(-y) = ±ψc∕v(y)). Therefore, the momentum matrix elements are non-zero for interband-transitions from the symmetric (anti-symmetric) to the symmetric (anti-symmetric) wave functions. This transition rule results in transitions from subbands with odd (even) to odd (even) indices in AGNRs/BN, which is described later.
Figure. 3.2 shows the structure of an AGNR/BN represented by AGNRnccBNmbn, where ncc is the number of carbon dimers in the unit cell of the AGNR and mbn = mbnu + mbnl is the summation of the upper and lower BNNRs dimers.

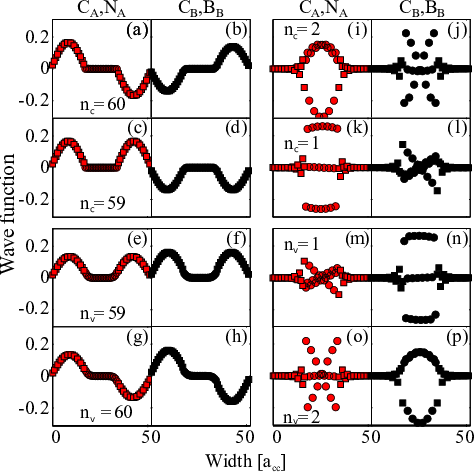
The wave functions at the sublattices A and B of an AGNR20BN40 at kx = 0 are shown in Fig. 3.3. CA∕B, NA∕B, and BA∕B represent the components of the wave functions at a carbon, nitrogen, and boron atom at some sublattice A or B. The wave function of each subband is the summation of the wave functions at these two sublattices. For example, the wave functions for the subband indices nv = 60 (Fig. 3.3(g) and (h)), nc = 2 (Fig. 3.3(i) and (j)), and nc = 60 (Fig. 3.3(a) and (b)) are anti-symmetric. Therefore, as discussed before, the matrix elements are non-zero for transitions from nv = 60 to nc = 2 and nc = 60. The transitions from nv = 59 to nc = 1 and nc = 59 are also possible as their respective wave functions are symmetric. With the same analysis, a transition from the highest valence subband to the lowest conduction subband (nv = 1 to nc = 1) is possible in AGNRs/BN, see Fig. 3.3(m) and (n) and Fig. 3.3(k) and (l).
To obtain the transition rules, momentum matrix elements should be calculated. The total wave functions of the system is given by [167]
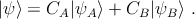 | (3.18) |
The Bloch wavefunctions |ψA⟩ and |ψB⟩ can be expressed as a linear combination of atomic wavefunctions of 2pz orbitals |Ap⟩ and |Bq⟩. Due to translational invariance along the x direction one obtains
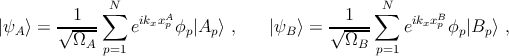 | (3.19) |
where ΩA∕B are the normalization factors, N is the number of A and B sublattices in the unit-cell of the GNR, xpA∕B are the x-positions of the pth A∕B-type carbon atom, ϕp is the y direction component of the wavefunctions at the pth lattice site. We impose hard-wall boundary conditions [168] at the edges, ϕ0 = 0 and ϕN+1 = 0. Therefore, one can assume that the component of the wavefunctions in the y direction form standing waves
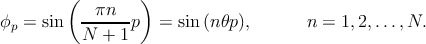 | (3.20) |
where n is the band index. For convenience the notation θ = π∕(N + 1) is introduced. Assuming the normalization condition ⟨ψA|ψA⟩ = ⟨ψB|ψB⟩ = 1, [168] the prefactors are obtained as ΩA = ΩB = Nx(N + 1)∕2, where Nx is the number of unit cells along the x direction. For a perfect and uniform ribbon we just need to perform the calculations over one unit-cell, therefore, from here on we assume Nx = 1. Finally, the coefficients CA and CB in Eq. 3.18 are found by solving the Schršodinger equation, H|ψ⟩ = E|ψ⟩, resulting in CB = ±CAe-iφn(kx), where φn(kx) is defined as
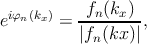 | (3.21) |
in which fn(kx) = eikxacc + 2e-ikxacc∕2 cos 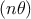 . To satisfy the normalization condition,
|CA|2 + |C
B|2 = 1, one can choose C
A = 1∕
. To satisfy the normalization condition,
|CA|2 + |C
B|2 = 1, one can choose C
A = 1∕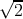 and CB = ±e-φn(kx)∕
and CB = ±e-φn(kx)∕ . The
wavefunction is given by
. The
wavefunction is given by
![[ ∑N ( )]
|±,n, k ⟩ = ∘---1----- eikxxAp sin (nθp)|A ⟩ ∓ e-iφn(kx)eikxxBp sin (nθp )|B ⟩ ,
x (N + 1) p p
p=1](diss97x.png) | (3.22) |
where the notation |±,n,kx⟩≡|ψn±(k x)⟩ is introduced and ± denote the conduction and the valence bands, respectively.
Based on Eq. 3.22, one can approximate the wave functions of an H-AGNR at pth atomic site with sin(nθp) functions, where n is the subband index and θ = π∕(N + 1). Considering such wave functions, the momentum matrix elements are
![[ ]
---1----im0- ∑N
pn,m (kx) = (N + 1) ℏ tacc sin (nθp) sin (m θp) Fn,m (kx).
p=1](diss98x.png) | (3.23) |
According to this equation, only transitions between valence and conduction subbands with the same band-index are allowed (shown in Appendix A). As shown in Fig. 3.3, the wave functions for AGNRs/BN are not necessarily a single sinusoidal function. The Fourier series of these wave functions contain sinusoidal functions with different arguments and coefficients, which results in more allowed interband-transitions compared to H-AGNRs. Non-zero terms and the symmetry properties of the AGNR/BN wave functions indicate that the interband-transitions between subbands with the same parity are allowed (odd to odd and even to even). This transition rule is more restricted for conventional H-AGNRs where the wave functions consist of complete sine terms (see Eq. A.5) [169]. The rules are also different from that of ZGNRs where interband-transitions from subbands with odd (even) indices to subbands with even (odd) indices are allowed. [170].